Question

【题目】已知，如图，二次函数（其中，是常数，为正整数）

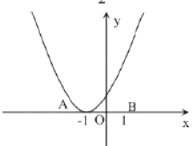
（1）若经过点求的值．

（2）当，若与轴有公共点时且公共点的横坐标为非零的整数，确定的值；

（3）在（2）的条件下将的图象向下平移个单位，得到函数图象，求的解析式；

（4）在（3）的条件下，将的图象在轴下方的部分沿轴翻折，图象的其余部分保持不变，得到一个新的图象，请结合新的图象解答问题，若直线与有两个公共点时，请直接写出的取值范围．

Answer 1

【答案】（1）；（2）；（3）；（4）或．

【解析】

（1）把代入，即可求出的值；

（2）把代入得到函数解析式，根据与轴有公共点，得出，结合k为正整数求出k的取值范围，根据与轴公共点的横坐标为非零的整数，进一步确定k即可；

（3）将解析式配方成顶点式，根据平移规律“上加下减”得出的解析式，整理为一般式即可；

（4）根据题目要求，画出的图像，并求出翻折部分解析式，求出经过D、E时b的值，再求出与只有一个公共点时b的值，结合图像即可确定b的取值范围．

解：（1）把代入得，

解得；

（2）当时，函数解析式为，

∵ 与轴有公共点，

∴，

∴，

∵ 为正整数

∴或

当时，函数解析式为，函数与轴交点为(),(),不合题意，舍去；

当函数解析式为，函数与轴交点为(),符合题意；

∴当，函数与轴有公共点且公共点的横坐标为非零的整数时，；

（3）由题意得解析式为：，

∴M的解析式为；

（4）当y=0时， 解得，

∴点D坐标为()，点E坐标为()．

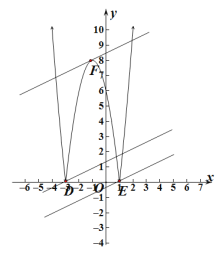
如图，将的图象在轴下方的部分沿轴翻折，解析式为，

即

当直线经过点E时，，，

当直线经过点D时，，；

当直线与有一个交点时，

，即 ，

∴，

解得，

∴若直线与有两个公共点时，则的取值范围为或．