题目内容
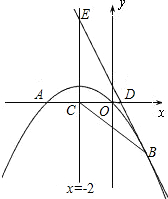
 如图,已知抛物线经过点A(-3,0),B(0,3),C(2,0)三点.
如图,已知抛物线经过点A(-3,0),B(0,3),C(2,0)三点.(1)求此抛物线的解析式;
(2)如果点D(1,m)在这条抛物线上,求m的值的点D关于这条抛物线对称轴的对称点E的坐标,并求出tan∠ADE的值.
分析:(1)设出交点式解析式,把B坐标代入即可;
(2)把点D的横坐标代入(1)中所求的解析式,就能求得m.进而求得点E.点D和E的纵坐标相等,那么DE∥AC,∴∠ADE=∠DAC,求得tan∠DAC的值就求得了tan∠ADE的值.
(2)把点D的横坐标代入(1)中所求的解析式,就能求得m.进而求得点E.点D和E的纵坐标相等,那么DE∥AC,∴∠ADE=∠DAC,求得tan∠DAC的值就求得了tan∠ADE的值.
解答:解:(1)设所求函数解析式为y=a(x+3)(x-2)
∵B(0,3)在所求函数解析式上
∴-6a=3,
a=-0.5
∴y=-0.5×(x+3)(x-2);
(2)∵D(1,m)在这条抛物线上
∴当x=1时,m=-0.5×4×(-1)=2
∵对称轴x=
=-0.5
∴点E的横坐标为-0.5-[1-(-0.5)]=-2.
∴点E的坐标为(-2,2)
做DF⊥AC于点F,
∵点D和E的纵坐标相等,
∴DE∥AC,
∴∠ADE=∠DAC
∴tan∠ADE=tan∠DAC=DF:AF=2:[1-(-3)]=
.
∵B(0,3)在所求函数解析式上
∴-6a=3,
a=-0.5
∴y=-0.5×(x+3)(x-2);
(2)∵D(1,m)在这条抛物线上
∴当x=1时,m=-0.5×4×(-1)=2
∵对称轴x=
| -3+2 |
| 2 |
∴点E的横坐标为-0.5-[1-(-0.5)]=-2.
∴点E的坐标为(-2,2)
做DF⊥AC于点F,
∵点D和E的纵坐标相等,
∴DE∥AC,
∴∠ADE=∠DAC
∴tan∠ADE=tan∠DAC=DF:AF=2:[1-(-3)]=
| 1 |
| 2 |
点评:本题考查用待定系数法求函数解析式,出现与x轴的两个交点时,一般应用交点式表示函数解析式.注意把所求的角的转移为易求得的三角函数的角.

练习册系列答案
 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
 2x+1经过抛物线上一点B(2,m),且与y轴.直线x=-2分别交于点D、E.
2x+1经过抛物线上一点B(2,m),且与y轴.直线x=-2分别交于点D、E. (2013•衡阳)如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=-1.
(2013•衡阳)如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=-1. 如图,已知抛物线经过原点O和x轴上另一点A,它的对称轴x=2与x轴交于点C,直线y=-2x-1经过抛物线上一点B(-2,m),且与y轴、直线x=2分别交于点D、E,
如图,已知抛物线经过原点O和x轴上另一点A,它的对称轴x=2与x轴交于点C,直线y=-2x-1经过抛物线上一点B(-2,m),且与y轴、直线x=2分别交于点D、E, 如图,已知抛物线经过坐标原点,与x轴的另一个交点为A,且顶点M坐标为(1,2),
如图,已知抛物线经过坐标原点,与x轴的另一个交点为A,且顶点M坐标为(1,2),