题目内容
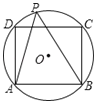
【题目】如图,矩形ABCD中,AB=8,AD=6,点O是对角线BD的中点,过点O的直线分别交AB、CD于点E、F.
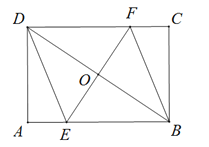
(1)求证:四边形DEBF是平行四边形;
(2)当四边形DEBF是菱形时,求EF的长.
【答案】(1)详见解析;(2)![]()
【解析】
(1)根据矩形的性质得到AB∥CD,由平行线的性质得到∠DFO=∠BEO,证明△DOF≌△BOE,根据全等三角形的性质得到DF=BE,于是证明四边形BEDF是平行四边形;
(2)根据四边形BEDF是菱形,得到DE=BE,EF⊥BD,OE=OF,设AE=x,则DE=BE=8-x根据勾股定理求出DE,BE,再求出BD,OD,最后根据勾股定理求出OE,EF,问题得解.
解:(1)证明:∵四边形ABCD是矩形,
∴AB∥CD,
∴∠DFO=∠BEO,
∵∠DOF=∠BOE ,OD=OB,
∴△DOF≌△BOE,
∴DF=BE,
∵DF∥BE,
∴四边形BEDF是平行四边形;
(2)∵四边形DEBF是菱形
∴DE=BE,EF⊥BD,OE=OF,
设AE=x,则DE=BE=8-x,
在Rt△ADE中,根据勾股定理得![]() ,
,
解得![]() ,
,
∴DE=BE=![]() ,
,
在Rt△ABD中,BD=![]() ,
,
∴OD=![]() ,
,
在Rt△EOD中,OE=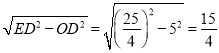 ,
,
∴EF=2OE= ![]() .
.

 轻巧夺冠周测月考直通中考系列答案
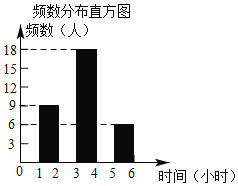
轻巧夺冠周测月考直通中考系列答案【题目】某中学兴趣小组为了解全校学生星期六和星期日在家使用手机的情况,兴趣小组随机抽取若干名学生,调查他们周末两天的使用手机时间,并根据调查结果绘制了下面两幅不完整的统计表和统计图.根据图表信息,解答下列问题:
阅读时间 (小时) | 频数 (人) | 频率 |
1≤x<2 | 9 | 0.15 |
2≤x<3 | a | m |
3≤x<4 | 18 | 0.3 |
4≤x<5 | 12 | n |
5≤x<6 | 6 | 0.1 |
合计 | b | 1 |
(1)填空:a= ,b= ,m= ,n= :
(2)将频数分布直方图补充完整;
(3)这个中学的学生共有1200人,根据上面信息来估算全校学生中周末两天使用手机时间不低于4小时的学生大约有多少人?