题目内容
【题目】如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFGH的一边FG在BC上,顶点E、H分别在AB、AC上,已知BC=40cm,AD=30cm.
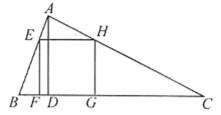
(1)求证:△AEH∽△ABC;
(2)求这个正方形的边长.
【答案】(1)详见解析;(2)正方形EFGH的边长为![]() cm
cm
【解析】
(1)根据EH∥BC得出△AEH∽△ABC;
(2)设AD与EH交于点M,证明四边形EFDM是矩形,设正方形边长为x,再利用△AEH∽△ABC,得![]() ,列出方程即可解决问题.
,列出方程即可解决问题.
(1)证明:∵四边形EFGH是正方形, ∴EH∥BC,
∴∠AEH=∠B,∠AHE=∠C, ∴△AEH∽△ABC.
(2)解:如图设AD与EH交于点M.

∵∠EFD=∠FEM=∠FDM=90°,
∴四边形EFDM是矩形, ∴EF=DM,设正方形EFGH的边长为x, ∵△AEH∽△ABC,
∴![]()
∴正方形EFGH的边长为![]() cm,
cm,

【题目】某地特产槟榔芋深受欢迎,某商场以7元/千克收购了3000千克优质槟榔芋,若现在马上出售,每千克可获得利润3元.根据市场调查发现,近段时间内槟榔芋的售价每天上涨0.2元/千克,为了获得更大利润,商家决定先贮藏一段时间后再出售.根据以往经验,这批槟榔芋的贮藏时间不宜超过100天,在贮藏过程中平均每天损耗约10千克.
(1)若商家将这批槟榔芋贮藏x天后一次性出售,请完成下列表格:
每千克槟榔芋售价(单位:元) | 可供出售的槟榔芋重量(单位:千克) | |
现在出售 | 3000 | |
x天后出售 |
(2)将这批槟榔芋贮藏多少天后一次性出售最终可获得最大利润?
【题目】如图,点P是![]() 上一动点,连接AP,作∠APC=45°,交弦AB于点C.已知AB=6cm,设A,P两点间的距离为xcm,P,C两点间的距离为y1cm,A,C两点间的距离为y2cm.(当点P与点A重合时,y1,y2的值为0;当点P与点B重合时,y1的值为0,y2的值为6).
上一动点,连接AP,作∠APC=45°,交弦AB于点C.已知AB=6cm,设A,P两点间的距离为xcm,P,C两点间的距离为y1cm,A,C两点间的距离为y2cm.(当点P与点A重合时,y1,y2的值为0;当点P与点B重合时,y1的值为0,y2的值为6).
小智根据学习函数的经验,分别对函数y随自变量x的变化而变化的规律进行了探究.
下面是小智的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了y与x的几组对应值;
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 0 | 1.21 | 2.09 | m | 2.99 | 2.82 | 0 |
y2/cm | 0 | 0.87 | 1.57 | 2.20 | 2.83 | 3.61 | 6 |
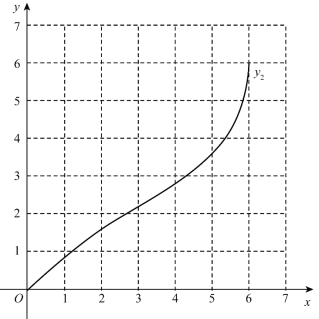
经测量m的值是 (保留一位小数).
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点(x,y1),(x,y2),并画出函数yspan>1,y2的图象;
(3)结合函数图象,解决问题:当△ACP为等腰三角形时,AP的长度约为 cm(保留一位小数).