题目内容
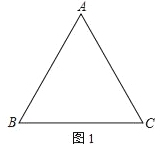
【题目】如图，△ABC是边长为6cm的等边三角形，点D从B点出发沿B→A方向在线段BA上以a cm/s速度运动，与此同时，点E从线段BC的某个端点出发，以b cm/s速度在线段BC上运动，当D到达A点后，D、E运动停止，运动时间为t（秒）．
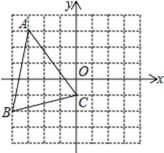
（1）如图1，若a=b=1，点E从C出发沿C→B方向运动，连AE、CD，AE、CD交于F，连BF．当0＜t＜6时：
①求∠AFC的度数；
②求
的值；
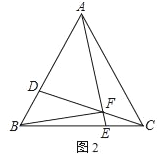
（2）如图2，若a=1，b=2，点E从B点出发沿B→C方向运动，E点到达C点后再沿C→B方向运动．当t≥3时，连DE，以DE为边作等边△DEM，使M、B在DE两侧，求M点所经历的路径长．
【答案】（1）①120°；②1；（2）当3≤t≤6时，M点所经历的路径长为3
．
【解析】
（1）①如图1，由题可得BD=CE=t，易证△BDC≌△CEA，则有∠BCD=∠CAE，根据三角形外角的性质可求得∠EFC=60°，即可得到∠AFC=120°；
②延长FD到G，使得FG=FA，连接GA、GB，过点B作BH⊥FG于H，如图2，易证△FAG是等边三角形，结合△ABC是等边三角形可证到△AGB≌△AFC，则有GB=FC，∠AGB=∠AFC=120°，从而可得∠BGF=60°．设AF=x，FC=y，则有FG=AF=x，BG=CF=y．在Rt△BHG中运用直角三角形的性质可得BH=
y，GH=
y，从而有FH=x﹣y．在Rt△BHF中根据勾股定理可得BF2=x2﹣xy+y2，代入所求代数式就可解决问题；
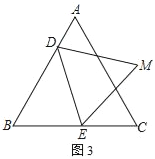
（2）过点E作EN⊥AB于N，连接MC，如图3，由题可得∠BEN=30°，BD=t，CE=2t﹣6，从而有BE=12﹣2t，BN=6﹣t，进而可得DN=EC．由△DEM是等边三角形可得DE=EM，∠DEM=60°，从而可得∠NDE=∠MEC，进而可证到△DNE≌△ECM，则有∠DNE=∠ECM=90°，故M点运动的路径为过点C垂直于BC的一条线段．
然后只需确定点M的始点和终点位置，就可解决问题．
（1）如图1，由题可得BD=CE=t．
∵△ABC是等边三角形，∴BC=AC，∠B=∠ECA=60°．
在△BDC和△CEA中，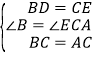
，∴△BDC≌△CEA，∴∠BCD=∠CAE，∴∠EFC=∠CAE+∠ACF=∠BCD+∠ACF=∠ACB=60°，∴∠AFC=120°；
②延长FD到G，使得FG=FA，连接GA、GB，过点B作BH⊥FG于H，如图2．
∵∠AFG=180°﹣120°=60°，FG=FA，∴△FAG是等边三角形，∴AG=AF=FG，∠AGF=∠GAF=60°．
∵△ABC是等边三角形，∴AB=AC，∠BAC=60°，∴∠GAF=∠BAC，∴∠GAB=∠FAC．
在△AGB和△AFC中，
，∴△AGB≌△AFC，∴GB=FC，∠AGB=∠AFC=120°，∴∠BGF=60°，∴∠GBH=30°．
设AF=x，FC=y，则有FG=AF=x，BG=CF=y．
在Rt△BHG中，GH=y，BH=y，∴FH=FG﹣GH=x﹣y．
在Rt△BHF中，BF2=BH2+FH2
=（y）2+（x﹣y）2=x2﹣xy+y2，∴
=
=1；
（2）过点E作EN⊥AB于N，连接MC，如图3，由题可得：∠BEN=30°，BD=1×t=t，CE=2（t﹣3）=2t﹣6，∴BE=6﹣（2t﹣6）=12﹣2t，BN=BE=6﹣t，∴DN=t﹣（6﹣t）=2t﹣6，∴DN=EC．
∵△DEM是等边三角形，∴DE=EM，∠DEM=60°．
∵∠NDE+∠NED=90°，∠NED+∠MEC=180°﹣30°﹣60°=90°，∴∠NDE=∠MEC．
在△DNE和△ECM中，∵
，∴△DNE≌△ECM，∴∠DNE=∠ECM=90°，∴M点运动的路径为过点C垂直于BC的一条线段．
当t=3时，E在点B，D在AB的中点，此时CM=EN=CD=BCsinB=6×=3；
当t=6时，E在点C，D在点A，此时点M在点C；
∴当3≤t≤6时，M点所经历的路径长为3．
