题目内容
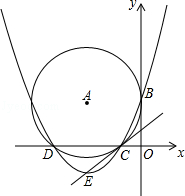
【题目】(本题共10分)如图,在平面直角坐标系中,![]() 与
与![]() 轴相交于
轴相交于![]() ,
,![]() 两点,与
两点,与![]() 轴相切于点
轴相切于点![]() .
.
(1)求经过![]() ,
,![]() ,
,![]() 三点的抛物线的函数表达式;
三点的抛物线的函数表达式;
(2)设抛物线的顶点为![]() ,证明:直线
,证明:直线![]() 与
与![]() 相切;
相切;
(3)在![]() 轴下方的抛物线上,是否存在一点
轴下方的抛物线上,是否存在一点![]() ,使
,使![]() 面积最大,最大值是多少?并求出点
面积最大,最大值是多少?并求出点![]() 的坐标.
的坐标.
【答案】(1)![]() ;
;
(2)∵![]() =
=![]() ,∴
,∴![]() ,
,
设直线![]() 的函数解析式为
的函数解析式为![]() ,
,
则 ,解得
,解得![]()
∴![]() ,
,
∵ 直线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,
∴在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
如图1,连接![]() ,
,![]() ,
,![]() ,
,
则![]() ,
, ![]() =
= ![]()
![]()
∴![]() ,
,![]() .......... (1分)
.......... (1分)
在![]() 与
与![]() 中,
中,
∵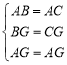 ,
,
∴![]() ,
,
∴![]() .......... (2分)
.......... (2分)
∵![]() 与
与![]() 轴相切于点
轴相切于点![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵点![]() 在
在![]() 上,
上,
∴直线![]() 与
与![]() 相切.......... (4分)
相切.......... (4分)
(3)存在,最大值是![]() ,
,![]() .
.
【解析】
试题分析:
(1)把![]() ,
,![]() ,
,![]() 代入二次函数的解析式即可得到结果;
代入二次函数的解析式即可得到结果;
(2)由![]()
![]() ,得到顶点
,得到顶点![]() 的坐标
的坐标![]() ,求得直线
,求得直线![]() 的解析式
的解析式![]() ,在
,在![]() 中,
中,![]() ,
,![]() ,∴
,∴![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,得
,得![]() ,
,![]() ,证得
,证得![]() ,得到
,得到![]() ,由于
,由于![]() 与
与![]() 轴相切于点
轴相切于点![]() ,于是得到
,于是得到![]() ,即可求得结论;
,即可求得结论;
(3)连接![]() ,
,![]() ,
,![]() ,设
,设![]() ,过
,过![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() ,求得直线
,求得直线![]() 的解析式为
的解析式为![]() ,得到点
,得到点![]() 的坐标为
的坐标为![]() ,于是得到
,于是得到![]() ,
,
推出![]() ,
,
即可得到结论.
试题解析:
解:(1)设抛物线的解析式为:![]() ,
,
把![]() ,
,![]() ,
,![]() 代入得
代入得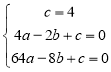 ,解得
,解得![]() .
.
∴经过![]() ,
,![]() ,
,![]() 三点的抛物线的函数表达式为:
三点的抛物线的函数表达式为:![]() .......... (1分)
.......... (1分)
(2)∵![]() =
=![]() ,∴
,∴![]() ,
,
设直线![]() 的函数解析式为
的函数解析式为![]() ,
,
则 ,解得
,解得![]()
∴![]() ,
,
∵ 直线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,
∴在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
如图1,连接![]() ,
,![]() ,
,![]() ,
,
则![]() ,
, ![]() =
= ![]()
![]()
∴![]() ,
,![]() .......... (1分)
.......... (1分)
在![]() 与
与![]() 中,
中,
∵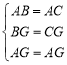 ,
,
∴![]() ,
,
∴![]() .......... (2分)
.......... (2分)
∵![]() 与
与![]() 轴相切于点
轴相切于点![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵点![]() 在
在![]() 上,
上,
∴直线![]() 与
与![]() 相切.......... (4分)
相切.......... (4分)

(3)存在点![]() ,使
,使![]() 面积最大.......... (1分)
面积最大.......... (1分)
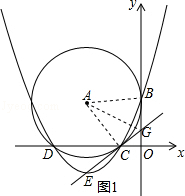
如图2连接![]() ,
,![]() ,
,![]() ,
,
设![]() ,
,
过![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() ,设直线
,设直线![]() 的解析式为
的解析式为![]() ,
,
则![]() ,解得
,解得![]() .
.
∴直线![]() 的解析式为
的解析式为![]() .......... (2分)
.......... (2分)
∴点![]() 的坐标为
的坐标为![]() ,
,
∴![]() ,
,
∴![]()
![]() .......... (3分)
.......... (3分)
∴当![]() 时,
时,![]() 最大,最大值是
最大,最大值是![]() .......... (4分)
.......... (4分)
当![]() 时,
时,![]() ,
,
∴![]() .......... (5分)
.......... (5分)

 字词句段篇系列答案
字词句段篇系列答案