Question

【题目】某公园有一座雕塑D，在北门B的正南方向，BD为100米，小树林A在北门的南偏西60°方向，荷花池C在北门B的东南方向，已知A，D，C三点在同一条直线上且BD⊥AC：

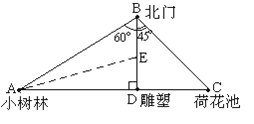
（1）分别求线段AB、BC、AC的长（结果中保留根号，下同）；

（2）若有一颗银杏树E恰好位于∠BAD的平分线与BD的交点，求BE的距离.

Answer 1

【答案】（1）、AB=200米；BC=100米；AC=(100+100)米；（2）、BE=(400－200)米.

【解析】

试题分析：（1）、根据Rt△ABD的三角函数得出AB、AD的长度，根据Rt△BCD的三角函数得出BC、DC的长度；（2）、过点E作EF⊥AB，从而得到AF和BF的长度，然后跟BE=2BF得出长度.

试题解析：（1）、AB＝200（米），BC＝100（米），

∵AD＝100，DC＝100，∴AC＝AD＋DC＝（100＋100）米

（2）、作EF⊥AB，

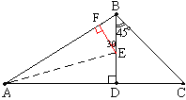
根据角平分线性质，得△AEF≌△AED ∴AF＝AD ＝100 又BE＝2BF

∴BE＝2（AB－AF）＝2（200－100）＝400－200＝（米）