题目内容
直线y= x+2与x轴、y轴分别交于A、B两点,D是x轴上一点,坐标为(x,0),△ABD的面积为S.
x+2与x轴、y轴分别交于A、B两点,D是x轴上一点,坐标为(x,0),△ABD的面积为S.
(1)求点A和点B的坐标;
(2)求S与x的函数关系式;
(3)当S=12时,求点D的坐标.
 x+2与x轴、y轴分别交于A、B两点,D是x轴上一点,坐标为(x,0),△ABD的面积为S.
x+2与x轴、y轴分别交于A、B两点,D是x轴上一点,坐标为(x,0),△ABD的面积为S.(1)求点A和点B的坐标;
(2)求S与x的函数关系式;
(3)当S=12时,求点D的坐标.
(1)(-4,0)和(0,2)(2)y=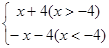 (3)(8,0)或(-16,0)
(3)(8,0)或(-16,0)
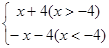 (3)(8,0)或(-16,0)
(3)(8,0)或(-16,0)(1)根据坐标轴上点的坐标特点分别令x=0求出y的值;再令y=0求出x的值即可求出A、B两点的坐标;
(2)根据三角形面积公式,再根据绝对值的性质即可求出S、x的关系式;
(3)由两点间的距离公式可知AD=|x+4|,再根据S=12即可求出x的值.
解:(1)A,B的坐标分别为(-4,0)和(0,2);
(2)S= AD·OB=
AD·OB= |x-(-4)|×2=|x+4|,也可以等于
|x-(-4)|×2=|x+4|,也可以等于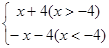 );
);
(3)由题意知|x+4|=12,解得x=8或x=-16,即D的坐标为(8,0)或(-16,0)
(2)根据三角形面积公式,再根据绝对值的性质即可求出S、x的关系式;
(3)由两点间的距离公式可知AD=|x+4|,再根据S=12即可求出x的值.
解:(1)A,B的坐标分别为(-4,0)和(0,2);
(2)S=
 AD·OB=
AD·OB= |x-(-4)|×2=|x+4|,也可以等于
|x-(-4)|×2=|x+4|,也可以等于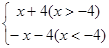 );
);(3)由题意知|x+4|=12,解得x=8或x=-16,即D的坐标为(8,0)或(-16,0)

练习册系列答案
相关题目

 和放水时间
和放水时间 之间的关系的是( )
之间的关系的是( )


 船在静水中航行的速度+水流速度,船逆流航行的速度
船在静水中航行的速度+水流速度,船逆流航行的速度 水流速度.】
水流速度.】 的距离是 。
的距离是 。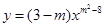 是正比例函数,则常数m的值是 。
是正比例函数,则常数m的值是 。