题目内容
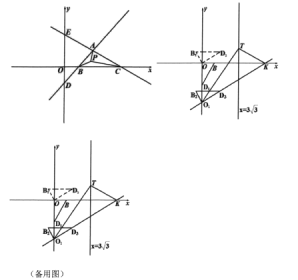
【题目】如图，在平面直角坐标系中，已知直线
与直线
相交于点
。
（1）求点的坐标；
（2）点
是
内部一点，连接
，求
的最小值；
（3）将点
向下平移一个单位得到点
，连接
，将
绕点
旋转至
的位置，使
轴，再将沿
轴上下平移得到
，在平移过程中，直线
与
轴交于点
，在直线
上任取一点
，连接
，
，
能否以
为直线边构成等腰直角三角形？若能，请直接写出所有符合条件的点的坐标，若不能，请说明理由。
【答案】（1）
；（2）
；（3）T1
，T2（
），T3（
）
【解析】
（1）列方程组求两个一次函数的交点坐标；（2）将△APC绕点C顺时针旋转60°，得到△DEC，连接BE，PD，则线段BE即为PA+PB+PC最小值的线段；(3)分四种情形：①当O1K=KT时，且O1在x轴下方，②当O1K=O1T时，且O1在x轴下方，③当O1K=KT时，且O1在x轴上方，④当O1K=O1T时，且O1在x轴上方，逐个进行计算即可．
解：（1）由题意可得：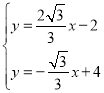
解得：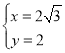
∴点A的坐标为
（2）如图2，将△APC绕点顺时针旋转60°得到△EDC，连接BE，PD．
在
中
当x=0时，y=4
当y=0时，
∴
∴∠ACB=30°
由旋转的性质可知：△PCD是等边三角形，
∴PC=PD，
∵PA=DE，
∴PA+PB+PC=DE+PB+PD，
∵DE+PB+PD≥BE，
∴当P，D在直线BE上时，PA+PB+PC的值最小，
∵在
中
当y=0时，
∴BC=CE=
，∠BCE=90°，
∵EB⊥BC，
∴BE=
BC=，
∴PA+PB+PC的最小值为．
（3）①当O1K=KT时，且O1在x轴下方，如图，则M（
）
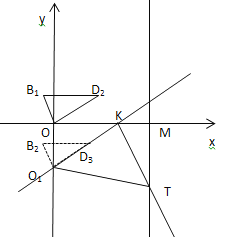
由题意可知：OB=OB1=
，OD=2，OD1=3
∴
∴∠OKO1=30°
∵
是等腰直角三角形
∴易证：△KTM≌△O1OK
∴OK=MT
设MT=t，则KM=
∴
解得：
∴T点坐标为（
）
②当O1K=O1T时，且O1在x轴下方，如图，作TN⊥y轴于N，
∵∠KON=∠TNO=∠TO1K=90°，
∴∠OO1K+∠O1KO=∠OO1K+∠TO1N=90°
∴∠O1KO=∠TO1N
∵O1K=O1T
∴△O1KO≌△TO1N（AAS）
∴OO1=TN=
∵∠OKO1=30°
即：
∴O1N=OK=9
∴ON=
∴T2（），
③当O1K=KT时，且O1在x轴上方，方法同①，此时，点T不存在；
④当O1K=O1T时，且O1在x轴上方，方法同②，可求得T3（）；
综上所述，使△O1KT成为以O1K为直角边的等腰直角三角形的点T的坐标为：T1，T2（），T3（）
