题目内容
【题目】某乡镇为解决抗旱问题,要在一河道上建一座水泵站,分别向河的同一侧两个村A与B供水.以河道上的大桥O为坐标原点,如图,以河道所在的直线为x轴建立直角坐标系。两村的坐标分别为A(2,3),B(12,7).
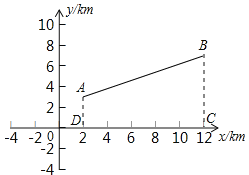
(1)求出水泵站建在距离大桥O多远的地方,可使所用输水管道最短?
(2)求出水泵站建在距离大桥O多远的地方,可使它到两村的距离相等?
【答案】(1)水泵站建在距离大桥5千米的地方,可使所用输水管道最短;(2)水泵站建在距离大桥9千米的地方,可使它到两村的距离相等.
【解析】
(1)为了使所修水泵站的所用输水管道最短,利用轴对称的方法画图可求;
(2)所求点要满足两个条件,到张村和李村的距离相等,可以作连接两村线段的垂直平分线,与x轴的交点即为所求.
(1)作点B关于x轴的对称点E,连接AE,则点E为(12,7)
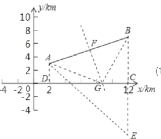
设直线AE的函数关系式为y=kx+b(k≠0),则
![]()
解得![]() ,
,
当y=0时,x=5.
所以,水泵站建在距离大桥5千米的地方,可使所用输水管道最短。
(2)作线段AB的垂直平分线GF,交AB于点F,交x轴于点G
设点G的坐标为(x,0)
在Rt△AGD中,AG![]() =AD
=AD![]() +DG
+DG![]() =3
=3![]() +(x2)
+(x2) ![]()
在Rt△BCG中,BG![]() =BC
=BC![]() +GC
+GC![]() =7
=7![]() +(12x)
+(12x) ![]()
∵AG=BG,
∴3![]() +(x2)
+(x2) ![]() =7
=7![]() +(12x)
+(12x) ![]()
解得x=9.
所以,水泵站建在距离大桥9千米的地方,可使它到两村的距离相等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目