题目内容
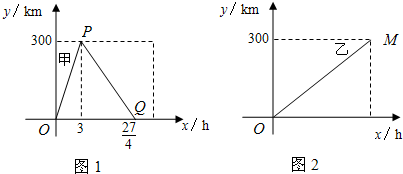
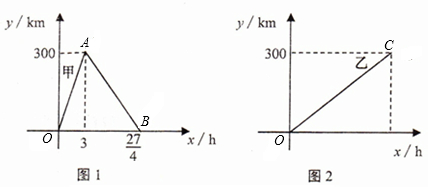
已知:甲、乙两车分别从相距300千米的A,B两地同时出发相向而行,甲到B地后立即返回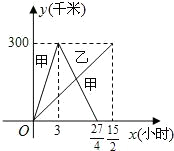 ,下图是它们离各自出发地的距离y(千米)与行驶时间x(小时)之间的函数图象.
,下图是它们离各自出发地的距离y(千米)与行驶时间x(小时)之间的函数图象.(1)请直接写出甲、乙两车离各自出发地的距离y(千米)与行驶时间x(小时)之间的函数关系式,并标明自变量x的取值范围;
(2)它们在行驶的过程中有几次相遇?并求出每次相遇的时间.
分析:(1)依图可知y甲的函数关系式为分段函数,y乙=40x;
(2)如图可知甲与乙有两次相遇.分段列方程求解.
(2)如图可知甲与乙有两次相遇.分段列方程求解.
解答:解:(1)甲由3小时到
小时的速度是:
=80千米/小时.
y甲=
①,y乙=40x(0≤x≤
)②;(1分)
(2)由题意有两次相遇.(1分)
方法一:①当0≤x≤3时,100x+40x=300,解得x=
,(1分)
②当3<x≤
时,(540-80x)+40x=300,解得x=6,(1分)
综上所述,两车第一次相遇时间为第
小时,第二次相遇时间为第6小时.(1分)
方法二:设经过x小时两车首次相遇,
则40x+100x=300,解得x=
,
设经过x小时两车第二次相遇,
则80(x-3)=40x,解得x=6.
综上所述,两车第一次相遇时间为第
小时,第二次相遇时间为第6小时.
| 27 |
| 4 |
| 300 | ||
|
y甲=
|
| 15 |
| 2 |
(2)由题意有两次相遇.(1分)
方法一:①当0≤x≤3时,100x+40x=300,解得x=
| 15 |
| 7 |
②当3<x≤
| 27 |
| 4 |
综上所述,两车第一次相遇时间为第
| 15 |
| 7 |
方法二:设经过x小时两车首次相遇,
则40x+100x=300,解得x=
| 15 |
| 7 |
设经过x小时两车第二次相遇,
则80(x-3)=40x,解得x=6.
综上所述,两车第一次相遇时间为第
| 15 |
| 7 |
点评:本题重点考查了一次函数的图象及一次函数的应用,是一道难度中等的题目.

练习册系列答案
相关题目
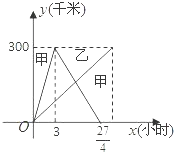 (千米)与行驶时间x(小时)之间的函数关系式,写出自变量的取值范围;
(千米)与行驶时间x(小时)之间的函数关系式,写出自变量的取值范围;