��Ŀ����
��֪����Rt��ABC��Rt��DEF����ͼ��1���ڷţ���C���E�غϣ�����B��C��E����F��ͬһ��ֱ���ϣ���ACB = ��EDF = 90�㣬��DEF = 45�㣬AC =" 8" cm��BC =" 6" cm��EF =" 9" cm��
��ͼ��2������DEF��ͼ��1����λ�ó�������1 cm/s���ٶ���CB���ABC�����ƶ����ڡ�DEF�ƶ���ͬʱ����P�ӡ�ABC�Ķ���B��������2 cm/s���ٶ���BA���A�����ƶ�������DEF�Ķ���D�ƶ���AC����ʱ����DEFֹͣ�ƶ�����PҲ��ֹ֮ͣ�ơ�DE��AC�ཻ�ڵ�Q������PQ�����ƶ�ʱ��Ϊt��s����0��t��4.5��������������⣺
��1����tΪ��ֵʱ����A���߶�PQ�Ĵ�ֱƽ�����ϣ�
��2������PE�����ı���APEC�����Ϊy��cm2������y��t֮��ĺ�����ϵʽ���Ƿ����ijһʱ��t��ʹ���y��С�������ڣ����y����Сֵ���������ڣ�˵�����ɡ�
��3���Ƿ����ijһʱ��t��ʹP��Q��F������ͬһ��ֱ���ϣ������ڣ������ʱt��ֵ���������ڣ�˵�����ɡ���ͼ��3����ͬѧ������ʹ�ã�
(1)2����2�� ����t=3ʱ��y��С=
����t=3ʱ��y��С= .��3��1s.
.��3��1s.
���������������1����Ϊ��A���߶�PQ��ֱƽ�����ϣ����Եõ��߶���ȣ��ɵ�CE=CQ���ú�t��ʽ�ӱ�ʾ���������߶μ��ɵý⣻
��2����PM��BC�����ı��ε������ʾΪS��ABC-S��BPE������⣻
��3��������ڷ���������tֵ�������������ε����ʼ�����ã�
��1���ߵ�A���߶�PQ�Ĵ�ֱƽ�����ϣ�
��AP=AQ.
�ߡ�DEF=45�㣬��ACB=90�㣬��DEF����ACB����EQC=180�㣬
���EQC=45��.
���DEF=��EQC.
��CE=CQ��
������֪��CE=t��BP=2t��
��CQ =t.
��AQ=8��t.
��Rt��ABC�У��ɹ��ɶ����ã�AB="10cm" .
��AP=10��2t.
��10��2t=8��t.
��ã�t=2.
�𣺵�t=2sʱ����A���߶�PQ�Ĵ�ֱƽ������.
��2����P��PM��BE����BE��M��

�� .
.
��Rt��ABC��Rt��BPM�� ��
��
��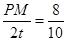 ��
��
��PM= .
.
��BC=6cm��CE=t��
��BE=6��t.
��y = S��ABC��S��BPE =
=
= .
.
�� ��
��
�������߿�������.
�൱t=3ʱ��y��С= .
.
�𣺵�t=3sʱ���ı���APEC�������С����С���Ϊ cm2��
cm2��
��3���������ijһʱ��t��ʹ��P��Q��F������ͬһ��ֱ����.
��P��PN��AC����AC��N��
�� .
.
�� ��
��
���PAN �ס�BAC.
�� .
.
�� .
.
�� ��
�� .
.
��NQ=AQ��AN��
��NQ=8��t��( ) =
) = ��
��
�ߡ�ACB=90�㣬B��C��E����F��ͬһ��ֱ���ϣ�
���QCF=90�㣬��QCF =��PNQ.
�ߡ�FQC =��PQN��
���QCF�ס�QNP .
��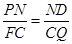 ��
��
�� ��
��
��
��
��ã�t=1.
�𣺵�t=1s����P��Q��F������ͬһ��ֱ���ϣ�
���㣺1.���κ�������ֵ��2.�߶δ�ֱƽ���ߵ����ʣ�3.���ɶ�����4.���������ε��ж������ʣ�

 ���㼤�������100�ִ��Ծ�ϵ�д�
���㼤�������100�ִ��Ծ�ϵ�д� x2��Ӧ�ĵ���Ϊ�� ����������y=4x2��Ӧ�ĵ���Ϊ�� ����������y=ax2��a��0����Ӧ�ĵ���Ϊ������������y=a��x��2��2+3��a��0����Ӧ�ĵ���Ϊ������
x2��Ӧ�ĵ���Ϊ�� ����������y=4x2��Ӧ�ĵ���Ϊ�� ����������y=ax2��a��0����Ӧ�ĵ���Ϊ������������y=a��x��2��2+3��a��0����Ӧ�ĵ���Ϊ������ ��a��0����Ӧ�ĵ���Ϊ6������x���ϣ���a��ֵ��
��a��0����Ӧ�ĵ���Ϊ6������x���ϣ���a��ֵ��

 ��m�dz�����
��m�dz����� ��ͼ�����C��0��1��������ΪQ��2��3����D��x���������ϣ����߶�OD=OC
��ͼ�����C��0��1��������ΪQ��2��3����D��x���������ϣ����߶�OD=OC


