题目内容
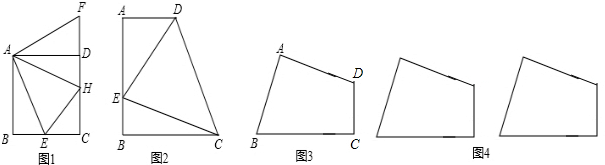
如图1,在正方形ABCD中,∠ECF的两边分别交边AB、AD于点E、F,且∠ECF=45°.

(1)①求证:BE+DF=EF;
②运用①的结论解决下面问题:如图2,在直角梯形ABCF中,AF∥BC(BC>AF),∠B=90°,AB=BC,E是AB上一点,且∠FCE=45°,BE=1.5,EF=2.5,求梯形ABCF的面积;
(2)在图1中,对角线AC、BD相交于点O,BD与CF分别交于点N,连接EN得到图3.当∠ECF绕点C旋转时,△ECN是什么特殊的三角形?请说明理由.

(1)①求证:BE+DF=EF;
②运用①的结论解决下面问题:如图2,在直角梯形ABCF中,AF∥BC(BC>AF),∠B=90°,AB=BC,E是AB上一点,且∠FCE=45°,BE=1.5,EF=2.5,求梯形ABCF的面积;
(2)在图1中,对角线AC、BD相交于点O,BD与CF分别交于点N,连接EN得到图3.当∠ECF绕点C旋转时,△ECN是什么特殊的三角形?请说明理由.
分析:(1)①把△BCE绕点C顺时针旋转90°得到△CDG,根据旋转的性质可得BE=DG,CE=CG,∠BCE=∠DCG,然后求出∠FCG=45°,从而得到∠ECF=∠FCG,再利用“边角边”证明△ECF和△GCF全等,根据全等三角形对应边相等可得EF=GF,再求出GF=BE+DF即可得证;
②设正方形ABCD的边长为x,表示出AE,再根据①的结论表示出AF,然后在Rt△AEF中,利用勾股定理列出方程求解即可得到x的值,再求出AF,然后利用梯形的面积公式列式计算即可得解;
(2)根据正方形的对角线平分一组对角可得∠EBN=∠CBD=45°,然后求出B、C、E、N四点共圆,再根据同弧所对的圆周角相等可得∠CEN=∠CBD=45°,根据三角形内角和定理求出∠CNE=90°,从而得到△ECN是等腰直角三角形.
②设正方形ABCD的边长为x,表示出AE,再根据①的结论表示出AF,然后在Rt△AEF中,利用勾股定理列出方程求解即可得到x的值,再求出AF,然后利用梯形的面积公式列式计算即可得解;
(2)根据正方形的对角线平分一组对角可得∠EBN=∠CBD=45°,然后求出B、C、E、N四点共圆,再根据同弧所对的圆周角相等可得∠CEN=∠CBD=45°,根据三角形内角和定理求出∠CNE=90°,从而得到△ECN是等腰直角三角形.
解答: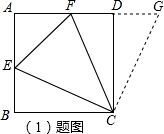 (1)①证明:如图,把△BCE绕点C顺时针旋转90°得到△CDG,
(1)①证明:如图,把△BCE绕点C顺时针旋转90°得到△CDG,
由旋转的性质可得BE=DG,CE=CG,∠BCE=∠DCG,
∵∠ECF=45°,
∴∠FCG=∠FCD+∠DCG=∠FCD+∠BCE=∠BCD-∠ECF=90°-45°=45°,
∴∠ECF=∠FCG,
在△ECF和△GCF中,
,
∴△ECF≌△GCF(SAS),
∴EF=GF,
∵GF=DG+DF=BE+DF,
∴BE+DF=EF;
②解:设正方形ABCD的边长为x,
∵BE=1.5,
∴AE=x-1.5,
∵EF=2.5,
∴AF=x-(EF-BE)=x-(2.5-1.5)=x-1,
在Rt△AEF中,AE2+AF2=EF2,
即(x-1.5)2+(x-1)2=2.52,
整理得,2x2-5x-3=0,
解得x1=3,x2=-
(舍去),
所以,AF=3-1=2,
梯形ABCF的面积=
×(2+3)×3=
;
(2)△ECN是等腰直角三角形.
理由如下:在正方形ABCD中,∠EBN=∠CBD=45°,
又∵∠ECF=45°,
∴∠ECN=∠ECF,
∴B、C、E、N四点共圆,
∴∠CEN=∠CBD=45°,
∴∠CEN=∠ECN=45°,
在△CEN中,∠CNE=180°-∠CEN-∠ECN=180°-45°-45°=90°,
∴△ECN是等腰直角三角形.
 (1)①证明:如图,把△BCE绕点C顺时针旋转90°得到△CDG,
(1)①证明:如图,把△BCE绕点C顺时针旋转90°得到△CDG,由旋转的性质可得BE=DG,CE=CG,∠BCE=∠DCG,
∵∠ECF=45°,
∴∠FCG=∠FCD+∠DCG=∠FCD+∠BCE=∠BCD-∠ECF=90°-45°=45°,
∴∠ECF=∠FCG,
在△ECF和△GCF中,
|
∴△ECF≌△GCF(SAS),
∴EF=GF,
∵GF=DG+DF=BE+DF,
∴BE+DF=EF;
②解:设正方形ABCD的边长为x,
∵BE=1.5,
∴AE=x-1.5,
∵EF=2.5,
∴AF=x-(EF-BE)=x-(2.5-1.5)=x-1,
在Rt△AEF中,AE2+AF2=EF2,
即(x-1.5)2+(x-1)2=2.52,
整理得,2x2-5x-3=0,
解得x1=3,x2=-
| 1 |
| 2 |
所以,AF=3-1=2,
梯形ABCF的面积=
| 1 |
| 2 |
| 15 |
| 2 |
(2)△ECN是等腰直角三角形.
理由如下:在正方形ABCD中,∠EBN=∠CBD=45°,
又∵∠ECF=45°,
∴∠ECN=∠ECF,
∴B、C、E、N四点共圆,
∴∠CEN=∠CBD=45°,
∴∠CEN=∠ECN=45°,
在△CEN中,∠CNE=180°-∠CEN-∠ECN=180°-45°-45°=90°,
∴△ECN是等腰直角三角形.
点评:本题是四边形综合题型,主要考查了正方形的性质,旋转的性质,全等三角形的判定与性质,勾股定理的应用,(2)利用四点共圆求解更加简便.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
 构造一个与上述命题类似的正确命题并加以证明.
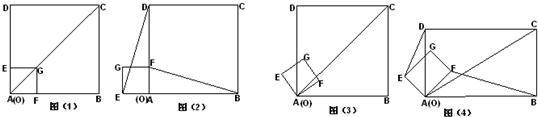
构造一个与上述命题类似的正确命题并加以证明.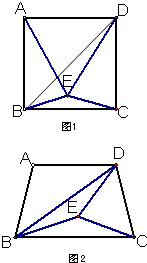 26、如图1,在正方形ABCD中,若点E是△DBC内的一点,且DE=DC,BE=CE.
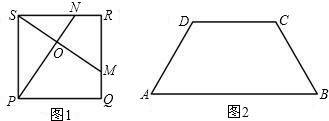
26、如图1,在正方形ABCD中,若点E是△DBC内的一点,且DE=DC,BE=CE.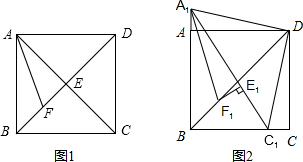 如图1,在正方形ABCD中,对角线AC与BD相交于点E,AF平分∠BAC,交BD于点F.
如图1,在正方形ABCD中,对角线AC与BD相交于点E,AF平分∠BAC,交BD于点F.