题目内容
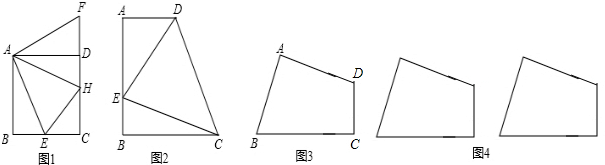
 26、如图1,在正方形ABCD中,若点E是△DBC内的一点,且DE=DC,BE=CE.
26、如图1,在正方形ABCD中,若点E是△DBC内的一点,且DE=DC,BE=CE.(1)连接AE.说明△ABE≌△DCE的理由;
(2)求∠BDE与∠CDE度数的比值;
(3)拓展探索:若只将题中的条件“正方形ABCD”换成条件“梯形ABCD中,AD∥BC,AB=DC,2∠DBC=∠DCB”.如图2,研究∠BDE与∠CDE度数的比值是否与(2)中的结论相同,写出你的研究结果并说明理由.
分析:(1)根据三角形的判定定理SAS来证明△ABE≌△DCE;
(2)根据正方形的对角线平分对角的性质求得∠ADB的值,然后由已知条件推出点E是边BC中线上的一点,知△AED是等边三角形,最后求出∠BDE与∠CDE度数并求比值;
(3)首先根据等腰梯形及等腰三角形的性质性质,可以推出△ADE是等边三角形.如果∠DBC=a,则∠DCB=2a,∠BDE=60°-a,∠CDE=120°-2a,所以比值依然是1:2.
(2)根据正方形的对角线平分对角的性质求得∠ADB的值,然后由已知条件推出点E是边BC中线上的一点,知△AED是等边三角形,最后求出∠BDE与∠CDE度数并求比值;
(3)首先根据等腰梯形及等腰三角形的性质性质,可以推出△ADE是等边三角形.如果∠DBC=a,则∠DCB=2a,∠BDE=60°-a,∠CDE=120°-2a,所以比值依然是1:2.
解答:解:(1)∵四边形ABCD是正方形,
∴AB=DC,∠ABC=∠DCB;
又∵BE=CE,
∴∠EBC=ECB(等腰对等角),
∴∠ABE=∠DCE;
∴△ABE≌△DCE;
(2)∵BE=CE,
∴点E在边BC的中线上,
∴AE=DE;
又∵DE=DC,AD=DC,
∴AE=DE=AD,
∴∠ADE=60°;
∵∠ADB=45°,∠BDE=∠ADE-∠ADB,
∴∠BDE=15°;
∵∠CDE=∠CDB-∠BDE,∠CDB=45°,
∴∠CDE=30°;
∴∠BDE:∠CDE=1:2;
(3)相同.
证明:连接AE.
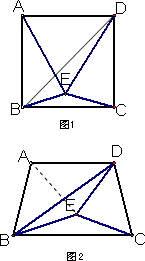 ∵AD∥BC,
∵AD∥BC,
∠DBC=∠ADB(两直线平行,内错角相等),
∵四边形ABCD是等腰梯形,
∴∠ABC=∠BCD;
又∵2∠DBC=∠DCB,
∴∠ABD=∠DBC;
∴∠ADB=∠ABD,
∴AB=AD;
∵DE=DC,AB=DC,又由(2)知,AE=ED,
∴AE=ED=AD,
∴三角形AED是等边三角形;
∴∠ADE=60°;
∵∠ADB=45°,∠BDE=∠ADE-∠ADB,
∴∠BDE=15°;
∵∠CDE=∠CDB-∠BDE,∠CDB=45°,
∴∠CDE=30°;
∴∠BDE:∠CDE=1:2.
∴AB=DC,∠ABC=∠DCB;
又∵BE=CE,
∴∠EBC=ECB(等腰对等角),
∴∠ABE=∠DCE;
∴△ABE≌△DCE;
(2)∵BE=CE,
∴点E在边BC的中线上,
∴AE=DE;
又∵DE=DC,AD=DC,
∴AE=DE=AD,
∴∠ADE=60°;
∵∠ADB=45°,∠BDE=∠ADE-∠ADB,
∴∠BDE=15°;
∵∠CDE=∠CDB-∠BDE,∠CDB=45°,
∴∠CDE=30°;
∴∠BDE:∠CDE=1:2;
(3)相同.
证明:连接AE.
 ∵AD∥BC,
∵AD∥BC,∠DBC=∠ADB(两直线平行,内错角相等),
∵四边形ABCD是等腰梯形,
∴∠ABC=∠BCD;
又∵2∠DBC=∠DCB,
∴∠ABD=∠DBC;
∴∠ADB=∠ABD,
∴AB=AD;
∵DE=DC,AB=DC,又由(2)知,AE=ED,
∴AE=ED=AD,
∴三角形AED是等边三角形;
∴∠ADE=60°;
∵∠ADB=45°,∠BDE=∠ADE-∠ADB,
∴∠BDE=15°;
∵∠CDE=∠CDB-∠BDE,∠CDB=45°,
∴∠CDE=30°;
∴∠BDE:∠CDE=1:2.
点评:本题综合考查了正方形的性质、全等三角形的判定与性质.在解答此题时,要灵活运用正方形的边长、正三角形的角的特点.

练习册系列答案
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目

 构造一个与上述命题类似的正确命题并加以证明.
构造一个与上述命题类似的正确命题并加以证明.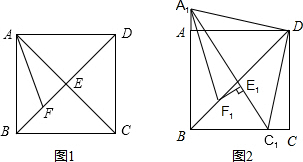 如图1,在正方形ABCD中,对角线AC与BD相交于点E,AF平分∠BAC,交BD于点F.
如图1,在正方形ABCD中,对角线AC与BD相交于点E,AF平分∠BAC,交BD于点F.