题目内容
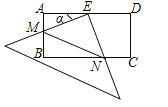
【题目】如图:在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连结AD、AG。
求证:(1)AD=AG,(2)AD与AG的位置关系如何。

【答案】(1)证明见解析(2)位置关系是AD⊥GA,利用见解析.
【解析】
试题分析:(1)先根据条件证明△BHF∽△CHE得出∠ABD=∠ACG,然后可证△ABD≌△GCA,从而可得AD=AG;(2)根据△ABD≌△GCA得出∠ADB=∠GAC,然后利用角的关系得出∠AED=∠GAD=90°,即可得证.
试题解析:(1)∵BE⊥AC,CF⊥AB,
∴∠HFB=∠HEC=90°,又∠BHF=∠CHE,
∴△BHF∽△CHE,
∴∠ABD=∠ACG,
在△ABD和△GCA中
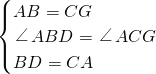 ,
,
∴△ABD≌△GCA(SAS),
∴AD=GA(全等三角形的对应边相等);
(2)位置关系是AD⊥GA,
理由为:∵△ABD≌△GCA,
∴∠ADB=∠GAC,
又∵∠ADB=∠AED+∠DAE,∠GAC=∠GAD+∠DAE,
∴∠AED=∠GAD=90°,
∴AD⊥GA.

练习册系列答案
相关题目