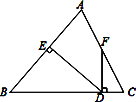
题目内容
【题目】已知四边形![]() 为菱形,
为菱形,![]() ,
,![]() ,
,![]() 的两边分别与射线
的两边分别与射线![]() 、
、![]() 相交于点
相交于点![]() 、
、![]() ,且
,且![]() .
.
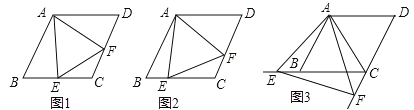
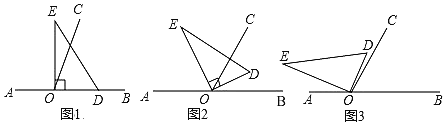
(1)如图1,当点![]() 是线段
是线段![]() 的中点时,请直接写出线段
的中点时,请直接写出线段![]() 与
与![]() 之间的数量关系;
之间的数量关系;
(2)如图2,当点![]() 是线段
是线段![]() 上的任意一点(点
上的任意一点(点![]() 不与点
不与点![]() 、
、![]() 重合)时,求证:
重合)时,求证:![]() ;
;
(3)如图3,当点![]() 在线段
在线段![]() 的延长线上,且
的延长线上,且![]() 时,求线段
时,求线段![]() 的长.
的长.
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() .
.
【解析】
(1)连接AC,先证△ABC是等边三角形,再由题意得出AE⊥BC,∠B=60°求解可得;
(2)证△BAE≌△CAF即可得;
(3)作AG⊥BC,由∠EAB=15°,∠ABC=60°知∠AEB=45°,根据AG=2![]() 得EG=AG=2
得EG=AG=2![]() ,EB=EG-BG=2
,EB=EG-BG=2![]() -2,再证△AEB≌△AFC知EB=FC,由FD=FC+CD=EB+CD可得答案.
-2,再证△AEB≌△AFC知EB=FC,由FD=FC+CD=EB+CD可得答案.
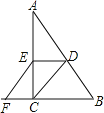
解:(1)如图1,连接AC,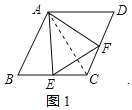
∵四边形ABCD是菱形,
∴AB=BC,
又∵∠ABC=60°,
∴△ABC是等边三角形,
∵E是BC中点,
∴AE⊥BC,BE=![]() BC=
BC=![]() AB
AB
在Rt△ABE中,AE=BEtanB=![]() BE;
BE;
(2)证明:连接![]() ,如图2中,
,如图2中,
∵四边形![]() 是菱形,
是菱形,![]() ,
,
∴![]() 与
与![]() 都是等边三角形,
都是等边三角形,
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
 ,
,
∴![]() .
.
∴![]() .
.

(3)解:连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,如图3所示,
,如图3所示,
∵![]() ,
,![]() ,
,
∴![]() .
.
在![]() 中,
中,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
在![]() 中,
中,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
由(2)得![]() ,
,![]() ,
,
则![]() ,
,
∵![]() ,
,
∴![]() ,
,
可得![]() ,
,
∴![]() ,
,
∴![]()
![]() .
.


练习册系列答案
相关题目