题目内容
【题目】以直线AB上一点O为端点作射线OC使∠BOC=60°,将一个直角三角形的直角顶点放在O处(注:∠DOE=90°).
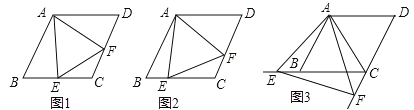
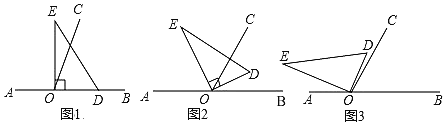
(1)如图1,若直角三角板DOE的一边OD放在射线OB上,则∠COE=______;
(2)如图2,将直角三角板DOE绕点O逆时针方向转动到某个位置,若OE恰好平分∠AOC,则∠BOD=______;
(3)如图3,将三角板DOE绕点O逆时针转动到某个位置时,若恰好∠COD=![]() ∠AOE,求∠BOD的度数.
∠AOE,求∠BOD的度数.
【答案】(1)30°;(2)∠COD=30°;(3)∠BOD的度数为65°.
【解析】
(1)代入∠BOE=∠COE+∠COB求出即可;
(2)求出∠AOE=∠COE,根据∠DOE=90°求出∠AOE+∠DOB=90°,∠COE+∠COD=90°,推出∠COD=∠DOB,即可得出答案;
(3)根据平角等于180°求出即可.
(1)∵∠BOE=∠COE+∠COB=90°,
又∵∠COB=60°,
∴∠COE=30°,
故答案为:30°;
(2)∵OE平分∠AOC,
∴∠COE=∠AOE=![]() ∠COA,
∠COA,
∵∠EOD=90°,
∴∠AOE+∠DOB=90°,∠COE+∠COD=90°,
∴∠COD=∠DOB=![]() ∠BOC=30°;
∠BOC=30°;
(3)设∠COD=x,则∠AOE=5x,
∵∠AOE+∠DOE+∠COD+∠BOC=180°,∠DOE=90°,∠BOC=60°,
∴5x+90°+x+60°=180°,
解得x=5°,
即∠COD=5°,
∴∠BOD=∠COD+∠BOC=5°+60°=65°,
∴∠BOD的度数为65°.

【题目】为缓解油价上涨给出租车行业带来的成本压力,某市拟调整出租车运价,调整方案见下列表格及图象(其中![]() 为常数)
为常数)
行驶路程 | 收费标准 | |
调价前 | 调价后 | |
不超过 | 起步价7元 | 起步价 |
超过 | 每公里2元 | 每公里 |
超出 | 每公里 | |
设行驶路程为![]() ,调价前的运价
,调价前的运价![]() (元),调价后运价
(元),调价后运价![]() (元),如图,折线
(元),如图,折线![]() 表示
表示![]() 与
与![]() 之间的函数关系式,线段
之间的函数关系式,线段![]() 表示当
表示当![]() 时,
时,![]() 与
与![]() 的函数关系式,根据图表信息,完成下列各题:
的函数关系式,根据图表信息,完成下列各题:
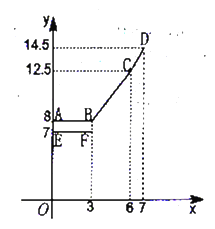
①填空:![]() ,
,![]() ,
,![]() ;
;
②当![]() 时,求
时,求![]() 与
与![]() 的关系,补充图中该函数的图像;
的关系,补充图中该函数的图像;
③函数![]() 与
与![]() 的图象是否存在交点?若存在,求出交点的坐标,并说明该点的实际意义;若不存在,请说明理由.
的图象是否存在交点?若存在,求出交点的坐标,并说明该点的实际意义;若不存在,请说明理由.