��Ŀ����
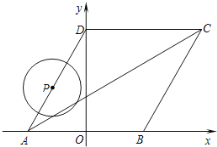
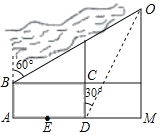
����Ŀ����ͼ��ʾ��С�����ڵ�O����������ѧУ��УΪ����ABCD��������AD��1000�ף��ϱ���AB��600�ף�ѧУ����������AD���е�E����BΪѧУ���������ţ�С���Ӽҵ�ѧУ��������·��·��O��M��E����M��90������Ҳ�������غӹ۹�·��·��O��B��С����D�����Oλ�ڱ�ƫ��30������B�����Oλ�ڱ�ƫ��60��С���Ӽҵ�ѧУ������·���У���·�߱ȶ�·�߶�_____�ף�������������ţ�
���𰸡�![]()
��������
��ͼ��������ã���OBF��30����DOM��30����FM��AB��600����DM��CF��x���õ�BF��1000+x����ֱ�������μ��ɵõ����ۣ�
�⣺��ͼ��������ã���OBF��30����DOM��30����FM��AB��600��
��DM��CF��x��
��BF��1000+x��
��Rt��BOF�У��ߡ�OBF��30����
��OF��![]() BF��
BF��![]() ��OB��
��OB�� ��
��
��Rt��ODM��DM��x��
��OM��![]() x��
x��
��OF��OM��FM��![]() x��600��
x��600��
��![]() ��
��![]() x��600��
x��600��
��ã�x��500+300![]() ��
��
��OF��500![]() +300��
+300��
��BO��2OF��1000![]() +600��
+600��
��·��O��M��E�ij��ȣ�500+x+![]() x��500+500+300
x��500+500+300![]() +500
+500![]() +900��1900+800
+900��1900+800![]() ��
��
�·�߱ȶ�·�߶ࣨ1300��200![]() ���ף�
���ף�
�ʴ�Ϊ��1300��200![]() ��
��


 ���㼤�������100�ִ��Ծ�ϵ�д�
���㼤�������100�ִ��Ծ�ϵ�д�