题目内容
【题目】设x1、x2是方程x2﹣4x+m=0的两个根,且x1+x2﹣x1x2=1,则x1+x2= , m= .
【答案】4;3
【解析】解:∵x1、x2是方程x2﹣4x+m=0的两个根,
∴x1+x2=﹣ ![]() =4,x1x2=
=4,x1x2= ![]() =m.
=m.
∵x1+x2﹣x1x2=4﹣m=1,
∴m=3.
所以答案是:4;3.
【考点精析】掌握根与系数的关系和代数式求值是解答本题的根本,需要知道一元二次方程ax2+bx+c=0(a≠0)的根由方程的系数a、b、c而定;两根之和等于方程的一次项系数除以二次项系数所得的商的相反数;两根之积等于常数项除以二次项系数所得的商;求代数式的值,一般是先将代数式化简,然后再将字母的取值代入;求代数式的值,有时求不出其字母的值,需要利用技巧,“整体”代入.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】老王有一批货物要从A地运往B地准备租用某汽车运输公司的甲、乙两种货车若干辆,经了解,这两种货车两次运载货物的情况如下表所示:(每次都是满载)
第一次 | 第二次 | |
甲 | 2辆 | 5辆 |
乙 | 3辆 | 6辆 |
累计货运量 | 15.5t | 35t |
(1)甲、乙两种货车每辆各可运货物多少吨?
(2)现老王租用该公司甲货车3辆,乙货车5辆,刚好将这批货物运完(满载)若每吨货的运费为30元,则老王应付运费多少元?
【题目】如图,已知△ABC内接于⊙O,点C在劣弧AB上(不与点A,B重合),点D为弦BC的中点,DE⊥BC,DE与AC的延长线交于点E,射线AO与射线EB交于点F,与⊙O交于点G,设∠GAB=ɑ,∠ACB=β,∠EAG+∠EBA=γ,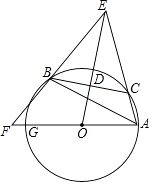
(1)点点同学通过画图和测量得到以下近似数据:
ɑ | 30° | 40° | 50° | 60° |
β | 120° | 130° | 140° | 150° |
γ | 150° | 140° | 130° | 120° |
猜想:β关于ɑ的函数表达式,γ关于ɑ的函数表达式,并给出证明:
(2)若γ=135°,CD=3,△ABE的面积为△ABC的面积的4倍,求⊙O半径的长.