题目内容
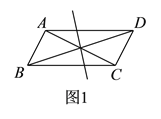
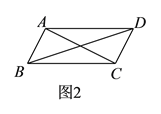
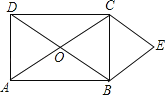
【题目】平行四边形ABCD的对角线AC和BD交于O点,分别过顶点B,C作两对角线的平行线交于点E,得平行四边形OBEC.
(1)如果四边形ABCD为矩形(如图),四边形OBEC为何种四边形?请证明你的结论;
(2)当四边形ABCD是 形时,四边形OBEC是正方形.
【答案】(1)证明见解析;(2)正方
【解析】(1)根据矩形的性质:两条对角线相等且互相平分,即可得到结论;(2)根据正方形的性质:对角线相等且互相垂直平分,即可得到结论.
解:(1)四边形OBEC是菱形.理由如下:
∵BE∥OC,CE∥OB,
∴四边形OBEC为平行四边形.
又∵四边形ABCD是矩形,
∴OC=![]() AC; OB=
AC; OB=![]() BD;AC=BD
BD;AC=BD
∴OC=OB,
∴平行四边形OBEC为菱形;
(2) 四边形ABCD是正方形时,四边形OBEC是正方形. 理由如下:
四边形OBEC是菱形.
∵BE∥OC,CE∥OB,
∴四边形OBEC为平行四边形.
又∵四边形ABCD是正方形,
∴OC=![]() AC; OB=
AC; OB=![]() BD;AC=BD且AC⊥BD
BD;AC=BD且AC⊥BD
∴OC=OB,∠BOC=90,
∴平行四边形OBEC为正方形;
即:当四边形ABCD是正方形时,四边形OBEC是正方形.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目