Question

【题目】如图所示，正五边形ABCDE的对角线AC、BE相交于M．

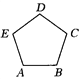
（1）求证：四边形CDEM是菱形；

（2）设MF2=BE·BM，若AB=4，求BE的长．

Answer 1

【答案】（1）证明见解析（2）2+2

【解析】试题分析：(1)先证明CDEM是平行四边形，由于DE=DC，所以是菱形.

(2) 先证明△ABE∽△MAB，得到AB2=BEBM；ME2=BEBM，可解得BE长..

试题解析：

（1）∵五边形ABCDE是正五边形，
∴∠D=××360°=108°，∠DCA=××360°=72°，
∴∠D+∠DCA=180°，
∴DE∥AC；同理可证DC∥BE，
∴四边形DEMC为平行四边形，而DE=DC，
∴四边形CDEM是菱形．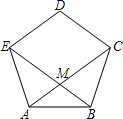

（2）∵五边形ABCDE是正五边形，
∴∠AEB=××360°=36°，∠EAM=××360°=72°；
同理可求∠BAC=∠ABE=36°，
∴△ABE∽△MAB，
∴AB：BE=BM：AB，
∴AB2=BEBM；
∵ME2=BEBM，
∴ME=AB=4，BM=BE-4，
∴BE（BE-4）=16，
解得：BE=2+2或2-2（舍去）．