��Ŀ����
����Ŀ����ƽ��ֱ������ϵ�У�O������ԭ�㣬����OABC��λ����ͼ��ʾ����A��C������ֱ�Ϊ��10��0������0��8������P��y���������ϵ�һ�����㣬����OAP��AP���۵õ���O��AP��ֱ��BC��ֱ��O��P���ڵ�E����ֱ��OA'���ڵ�F��
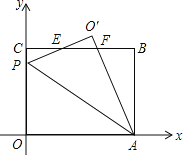
��1������P��y�������ᣬ����OAP=30��ʱ�����O������ꣻ
��2����O������ֱ��BC��ʱ����ֱ��O��A�Ľ���ʽ��
��3������P�ھ���OABC��OC���˶������У��Ƿ����ijһʱ�̣�ʹ���߶�CF���߶�OP�ij�����ȣ������ڣ���ֱ��д����P�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1����O�������Ϊ��5��5![]() ������2��ֱ��O��A�Ľ���ʽΪy=
������2��ֱ��O��A�Ľ���ʽΪy=![]() x��
x��![]() ����3������P�ھ���OABC��OC���˶������У�����ijһʱ�̣�ʹ���߶�CF���߶�OP�ij�����ȣ���P������Ϊ��0��
����3������P�ھ���OABC��OC���˶������У�����ijһʱ�̣�ʹ���߶�CF���߶�OP�ij�����ȣ���P������Ϊ��0��![]() ����0��
����0��![]() ����
����
��������
�����������1������O��O����O��G��OA�ڵ�G������AO=AO�䣬��O��AO=2��OPA=60�㣬���ɵó���O��AO�ǵȱ������Σ��ٽ�ϵ�A�����꼴�ɵó���O������ꣻ
��2����ֱ��O��A�Ľ���ʽΪy=kx+b�����ݹ��ɶ����ɵó�BO��ij��ȣ��ٸ���O�����߶�BC�Ϻ�O����CB�ӳ����Ϸ�����������ǣ��ɴ˼��ɵó���O������꣬��ϵ�AO����������ô���ϵ�������ɵó�ֱ��O��A�Ľ���ʽ��
��3��������ڣ����P��0��m�������ݵ�O����ֱ��BC�������������������ۣ�����ƽ���ߵ������ҳ���ȵĽǴӶ��ó������������ƣ��ٸ������������ε����ʣ���Ƚǵ����Ǻ���ֵ��ȣ��ҳ������֮��Ĺ�ϵ���ɴ˼����г�����m�ķ��̣��ⷽ�̼��ɵó����ۣ�
�⣺��1������O��O����O��G��OA�ڵ�G����ͼ1��ʾ��
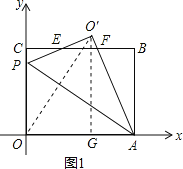
��O��AO=2��OPA=60�㣬AO=AO�䣬
���O��AO�ǵȱ������Σ�
����A��������10��0����
��OA=10��OG=![]() OA=5��O��G=
OA=5��O��G=![]() OA=5
OA=5![]() ��
��
����O���������5��5![]() ����
����
��2����ֱ��O��A�Ľ���ʽΪy=kx+b��
��Rt��ABO����AO��=10��AB=8��
��BO���T6��
�ٵ�O�����߶�BC��ʱ��CO��=10��6=4��
����O���������4��8����
����![]() ����ã�
����ã�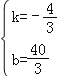 ��
��
����ʱֱ��O��A�Ľ���ʽΪy=��![]() x+
x+![]() ��
��
�ڵ�O����CB�ӳ�����ʱ��CO��=10+6=16��
����O���������16��8����
����![]() ����ã�
����ã�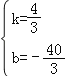
����ʱֱ��O��A�Ľ���ʽΪy=![]() x��
x��![]() ��
��
��3��������ڣ��ɵ�O���λ�ò�ͬ�����������
�ٵ���O����BC���Ϸ�ʱ�����P��0��m��������O����O��G��OA�ڵ�G������P��PQ��O��G�ڵ�Q����ͼ2��ʾ��

��OP=CF��
��BF=BC��CF=10��m��
����C��0��8����
��AB=OC=8��
��Rt��ABF��AB=8��BF=10��m��
��AF=![]() =
=![]() ��
��
��O��G��x�ᣬAB��OA��
��O��G��AB��
���O��GA�ס�ABF��
��![]() ��
��
��O��G=![]() ��AG=
��AG=![]() ��
��
��O��Q=O��G��OP=![]() ��m��PQ=OA��AG=10��
��m��PQ=OA��AG=10��![]() ��
��
�ߡ�PO��Q+��O��PQ=90�㣬��PO��Q+��AO��G=90�㣬
���O��PQ=��AO��G=��FAB��
��![]() ��
��
��PQ=![]() =10��
=10��![]() ��
��
��ã�m1=![]() ��m2=10��
��m2=10��
������m1=![]() �Ƿ�ʽ���̵Ľ⣬
�Ƿ�ʽ���̵Ľ⣬
��ʱ��P������Ϊ��0��![]() ����
����
�ڵ���O����BC���·�ʱ����AF��y��Ľ���ΪM����ͼ3��ʾ��

���P��0��m������CF=OP=m��
BF=10+m��AB=8��OA=10��AF=![]() =
=![]() ��
��
��BC��AO��
���AFB=��MAO��
��![]() ��
��
��OM=![]() ��
��
��PM=OM��OP=![]() ��m��
��m��
�ߡ�MPO������AMO���࣬
���MPO��=��AFB��
��![]() ����
����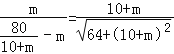 ��
��
��ã�m3=![]() ��m4=��10����ȥ����
��m4=��10����ȥ����
������m3=![]() �Ƿ�ʽ���̵Ľ⣬
�Ƿ�ʽ���̵Ľ⣬
��ʱ��P������Ϊ��0��![]() ����
����
���Ͽ�֪������P�ھ���OABC��OC���˶������У�����ijһʱ�̣�ʹ���߶�CF���߶�OP�ij�����ȣ���P������Ϊ��0��![]() ����0��
����0��![]() ����
����