题目内容
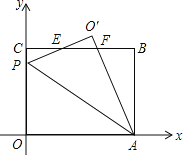
【题目】如图,在平面直角坐标系中,直线y=2x+b(b<0)与坐标轴交于A,B两点,与双曲线y=![]() (x>0)交于D点,过点D作DC⊥x轴,垂足为C,连接OD.已知△AOB∽△ACD,相似比为
(x>0)交于D点,过点D作DC⊥x轴,垂足为C,连接OD.已知△AOB∽△ACD,相似比为![]() .
.
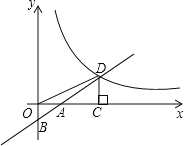
(1)如果b=﹣2,求k的值;
(2)试探究k与b的数量关系,并直接写出直线OD的解析式.
【答案】(1)k=12;(2)k=3b2.直线OD的解析式为:y=![]() x.
x.
【解析】
试题分析:(1)首先求出直线y=2x﹣2与坐标轴交点的坐标,然后由△AOB≌△ACD得到CD=OB,AO=AC,即可求出D坐标,由点D在双曲线y=![]() ( x>0)的图象上求出k的值;
( x>0)的图象上求出k的值;
(2)首先直线y=2x+b与坐标轴交点的坐标为A(﹣![]() ,0),B(0,b),再根据△AOB≌△ACD得到CD=DB,AO=AC,即可求出D坐标,把D点坐标代入反比例函数解析式求出k和b之间的关系,进而也可以求出直线OD的解析式.
,0),B(0,b),再根据△AOB≌△ACD得到CD=DB,AO=AC,即可求出D坐标,把D点坐标代入反比例函数解析式求出k和b之间的关系,进而也可以求出直线OD的解析式.
解:(1)当b=﹣2时,直线y=2x﹣2与坐标轴交点的坐标为A(1,0),B(0,﹣2).
∵△AOB∽△ACD,
∴CD=2OB,AO=2AC,
∴点D的坐标为(3,4).
∵点D在双曲线y=![]() ( x>0)的图象上,
( x>0)的图象上,
∴k=3×4=12.
(2)直线y=2x+b与坐标轴交点的坐标为A(﹣![]() ,0),B(0,b).
,0),B(0,b).
∵△AOB∽△ACD,
∴CD=2OB,AC=2AO,
∴点D的坐标为(![]() b,2b)
b,2b)
∵点D在双曲线y=![]() ( x>0)的图象上,
( x>0)的图象上,
∴k=(![]() )(2b)=3b2,即k与b的数量关系为:k=3b2.
)(2b)=3b2,即k与b的数量关系为:k=3b2.
直线OD的解析式为:y=![]() x.
x.

【题目】亚健康是时下社会热门话题,进行体育锻炼是远离亚健康的一种重要方式,为了解某市初中学生每天进行体育锻炼的时间情况,随机抽样调查了100名初中学生,根据调查结果得到如图所示的统计图表.
类别 | 时间t(小时) | 人数 |
A | t≤0.5 | 5 |
B | 0.5<t≤1 | 20 |
C | 1<t≤1.5 | a |
D | 1.5<t≤2 | 30 |
E | t>2 | 10 |
(1)a= ;
(2)补全条形统计图;
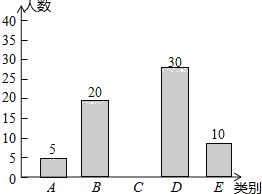
(3)据了解该市大约有30万名初中学生,请估计该市初中学生每天进行体育锻炼时间在1小时以上的人数.