题目内容
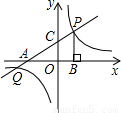
(2011•甘孜州)如图,直线y= x+1分别交x轴,y轴于点A,C,点P是直线AC与双曲线y=
x+1分别交x轴,y轴于点A,C,点P是直线AC与双曲线y= 在第一象限内的交点,PB⊥x轴,垂足为点B,△APB的面积为4.
在第一象限内的交点,PB⊥x轴,垂足为点B,△APB的面积为4.(1)求点P的坐标;
(2)求双曲线的解析式及直线与双曲线另一交点Q的坐标.
【答案】分析:(1)求出直线y= x+1与x轴,y轴于点A,C,根据点P在直线y=
x+1与x轴,y轴于点A,C,根据点P在直线y= x+1上,可设点P的坐标为(m,
x+1上,可设点P的坐标为(m, m+1),根据S△APB=
m+1),根据S△APB= AB•PB就可以得到关于m的方程,求出m的值.
AB•PB就可以得到关于m的方程,求出m的值.
(2)根据△APB的面积为4.就可以得到k=4,解反比例函数与一次函数解析式组成的方程组,就得到直线与双曲线的交点.
解答:解:(1)y= x+1,令x=0,则y=1;令y=0,则x=-2,
x+1,令x=0,则y=1;令y=0,则x=-2,
∴点A的坐标为(-2,0),点C的坐标为(0,1).(1分)
∵点P在直线y= x+1上,可设点P的坐标为(m,
x+1上,可设点P的坐标为(m, m+1),
m+1),
又∵S△APB= AB•PB=4,
AB•PB=4,
∴ (2+m)(
(2+m)( m+1)=4.(2分)
m+1)=4.(2分)
即:m2+4m-12=0,
∴m1=-6,m2=2.
∵点P在第一象限,
∴m=2.(3分)
∴点P的坐标为(2,2);(4分)
(2)∵点P在双曲线y=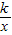 上,
上,
∴k=xy=2×2=4.(5分)
∴双曲线的解析式为y= .(6分)
.(6分)
解方程组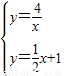 得
得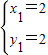 ,
, (8分)
(8分)
∴直线与双曲线另一交点Q的坐标为(-4,-1).(9分)
点评:本题主要考查了待定系数法求函数解析式,以及函数图象上的点与解析式的关系,图象上的点一定满足函数解析式.
 x+1与x轴,y轴于点A,C,根据点P在直线y=
x+1与x轴,y轴于点A,C,根据点P在直线y= x+1上,可设点P的坐标为(m,
x+1上,可设点P的坐标为(m, m+1),根据S△APB=
m+1),根据S△APB= AB•PB就可以得到关于m的方程,求出m的值.
AB•PB就可以得到关于m的方程,求出m的值.(2)根据△APB的面积为4.就可以得到k=4,解反比例函数与一次函数解析式组成的方程组,就得到直线与双曲线的交点.
解答:解:(1)y=
 x+1,令x=0,则y=1;令y=0,则x=-2,
x+1,令x=0,则y=1;令y=0,则x=-2,∴点A的坐标为(-2,0),点C的坐标为(0,1).(1分)
∵点P在直线y=
 x+1上,可设点P的坐标为(m,
x+1上,可设点P的坐标为(m, m+1),
m+1),又∵S△APB=
 AB•PB=4,
AB•PB=4,∴
 (2+m)(
(2+m)( m+1)=4.(2分)
m+1)=4.(2分)即:m2+4m-12=0,
∴m1=-6,m2=2.
∵点P在第一象限,
∴m=2.(3分)
∴点P的坐标为(2,2);(4分)
(2)∵点P在双曲线y=
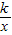 上,
上,∴k=xy=2×2=4.(5分)
∴双曲线的解析式为y=
 .(6分)
.(6分)解方程组
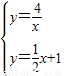 得
得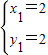 ,
, (8分)
(8分)∴直线与双曲线另一交点Q的坐标为(-4,-1).(9分)
点评:本题主要考查了待定系数法求函数解析式,以及函数图象上的点与解析式的关系,图象上的点一定满足函数解析式.

练习册系列答案
相关题目
 (2011•甘孜州)如图,平面直角坐标系中,OB在x轴上,∠ABO=90°,OB=1,OA=2.将△AOB绕点O逆时针旋转到△A′B′O,点A的对应点A′落在x轴上,B的对应点恰好落在双曲线
(2011•甘孜州)如图,平面直角坐标系中,OB在x轴上,∠ABO=90°,OB=1,OA=2.将△AOB绕点O逆时针旋转到△A′B′O,点A的对应点A′落在x轴上,B的对应点恰好落在双曲线 (2011•甘孜州)如图,四边形ABCD的对角线AC、BD互相垂直,则下列条件能判定四边形ABCD为菱形的是( )
(2011•甘孜州)如图,四边形ABCD的对角线AC、BD互相垂直,则下列条件能判定四边形ABCD为菱形的是( ) (2011•甘孜州)如图,在△ABC中,∠A=120°,AB=AC=4cm,⊙A与BC相切于点D,则⊙A的半径长为
(2011•甘孜州)如图,在△ABC中,∠A=120°,AB=AC=4cm,⊙A与BC相切于点D,则⊙A的半径长为