题目内容
（2011•甘孜州）如图，在△ABC中，∠A=120°，AB=AC=4cm，⊙A与BC相切于点D，则⊙A的半径长为2
2
cm．分析：连接AD．则由切线的性质△ABD是含30度角的直角三角形，然后通过“30度角所对的直角边是斜边的一半”来求AD的长度即可．
解答：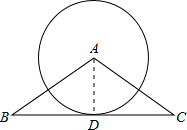
解：如图，连接AD．
∵⊙A与BC相切于点D，
∴AD⊥BC．
又∵AB=AC，
∴∠BAD=
∠BAC=60°，
∴在直角△ABD中，∠B=30°，
∴AD=
AB=2cm．
故答案是：2．
解：如图，连接AD．∵⊙A与BC相切于点D，
∴AD⊥BC．
又∵AB=AC，
∴∠BAD=
| 1 |
| 2 |
∴在直角△ABD中，∠B=30°，
∴AD=
| 1 |
| 2 |
故答案是：2．
点评：本题利用了切线的性质，等腰直角三角形的判定和性质求解．运用切线的性质来进行计算或论证，常通过作辅助线连接圆心和切点，利用垂直构造直角三角形解决有关问题．
练习册系列答案
相关题目
（2011•甘孜州）如图，平面直角坐标系中，OB在x轴上，∠ABO=90°，OB=1，OA=2．将△AOB绕点O逆时针旋转到△A′B′O，点A的对应点A′落在x轴上，B的对应点恰好落在双曲线
（2011•甘孜州）如图，四边形ABCD的对角线AC、BD互相垂直，则下列条件能判定四边形ABCD为菱形的是（ ）