题目内容
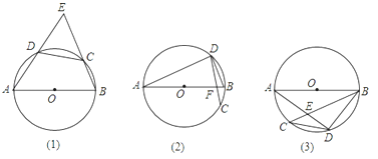
【题目】已知:如图1,在⊙O中,直径AB=4,CD=2,直线AD,BC相交于点E.
(1)∠E的度数为.
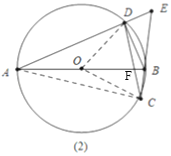
(2)如图2,AB与CD交于点F,请补全图形并求∠E的度数;
(3)如图3,弦AB与弦CD不相交,求∠AEC的度数.
【答案】(1)60°(2)60°(3)60°
【解析】
(1)连结OD,OC,BD,根据已知得到△DOC为等边三角形,由圆周角定理可得∠DBC=30°,根据直径所对的圆周角是直角,求出∠E的度数即可;(2)根据已知可得△DOC为等边三角形,根据圆周角定理可得∠DAC=30°,由圆内接四边形性质可得∠EBD=∠DAC=30°,根据直径所对的圆周角是直角,求出∠E的度数即可;(3)根据已知可得△DOC为等边三角形,根据圆周角定理可知∠CAD=30°,根据直径所对的圆周角是直角,求出∠AEC的度数即可;
(1)如图1,连结OD,OC,BD,
∵OD=OC=CD=2
∴△DOC为等边三角形,
∴∠DOC=60°
∴∠DBC=30°
∴∠EBD=30°
∵AB为直径,
∴∠ADB=90°
∴∠E=90°﹣30°=60°.

(2)①如图2,直线AD,CB交于点E,连结OD,OC,AC,.
∵OD=OC=CD=2,
∴△DOC为等边三角形,
∴∠DOC=60°,
∴∠DAC=30°,
∵∠EBD是圆内接四边形ACBD的外角,
∴∠EBD=30°,
∵AB为直径,
∴∠ACB=90°,
∴∠E=90°﹣30°=60°,
(3)如图3,连结OD,OC,AC,
∵OD=OC=CD=2,
∴△DOC为等边三角形,
∴∠DOC=60°,
∴∠CAD=30°,
∵AB是直径,∠ACB是AB所对的圆周角,
∴∠ACB=90°,
∴∠AEC=90°-30°=60°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目