题目内容
请仔细阅读材料,并解答相应问题:
定义A=a+b ,B=a-b
,B=a-b (a、b、m均为正有理数)都是无理数,若满足①A+B=2a为有理数;②AB=a2-mb2为有理数,则称A、B两数为姐妹数(如3+2
(a、b、m均为正有理数)都是无理数,若满足①A+B=2a为有理数;②AB=a2-mb2为有理数,则称A、B两数为姐妹数(如3+2 ,3-2
,3-2 ,∵3+2
,∵3+2 +3-2
+3-2 =6,(3+2
=6,(3+2 )(3-2
)(3-2 )=32-(2
)=32-(2 )2=9-8=1,∴6,1为有理数,则3
)2=9-8=1,∴6,1为有理数,则3 、3-2
、3-2 为姐妹数)
为姐妹数)
(1)已知x1,x2是x2-4x=2的两个根,求x1,x2的值,并通过以上方法判断x1,x2是否是一对姐妹数.
(2)在(1)条件下请继续判断x12、x22是否是一对姐妹数.
解:(1)方程x2-4x=2,
配方得:x2-4x+4=6,即(x-2)2=6,
∴x-2=± ,
,
解得:x1=2+ ,x2=2-
,x2=2- ,
,
∴x1+x2=2+ +2-
+2- =4,x1x2=(2+
=4,x1x2=(2+ )(2-
)(2- )=4-6=-2,
)=4-6=-2,
而4,-2都为有理数,∴x1,x2为姐妹数;
(2)∵x1+x2=4,x1x2=-2,
∴x12+x22=(x1+x2)2-2x1x2=16+4=20,x12+x22=(x1x2)2=4,而20与4都为有理数,
则x12、x22是一对姐妹数.
分析:(1)求出方程的解得到x1,x2的值,求出x1+x2与x1x2的值,利用题中的新定义判断即可;
(2)分别求出x12+x22与x12x22的值,利用题中的新定义判断即可.
点评:此题考查了分母有理化,二次根式有理化主要利用了平方差公式,所以一般二次根式的有理化因式是符合平方差公式的特点的式子.即一项符号和绝对值相同,另一项符号相反绝对值相同.
配方得:x2-4x+4=6,即(x-2)2=6,
∴x-2=±
 ,
,解得:x1=2+
 ,x2=2-
,x2=2- ,
,∴x1+x2=2+
 +2-
+2- =4,x1x2=(2+
=4,x1x2=(2+ )(2-
)(2- )=4-6=-2,
)=4-6=-2,而4,-2都为有理数,∴x1,x2为姐妹数;
(2)∵x1+x2=4,x1x2=-2,
∴x12+x22=(x1+x2)2-2x1x2=16+4=20,x12+x22=(x1x2)2=4,而20与4都为有理数,
则x12、x22是一对姐妹数.
分析:(1)求出方程的解得到x1,x2的值,求出x1+x2与x1x2的值,利用题中的新定义判断即可;
(2)分别求出x12+x22与x12x22的值,利用题中的新定义判断即可.
点评:此题考查了分母有理化,二次根式有理化主要利用了平方差公式,所以一般二次根式的有理化因式是符合平方差公式的特点的式子.即一项符号和绝对值相同,另一项符号相反绝对值相同.

练习册系列答案
相关题目
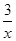 ﹥x+2的解集呢? 我们可以设
﹥x+2的解集呢? 我们可以设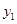 =
=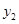 =x+2.然后求出它们的交点的坐标, 并在同一直角坐标系中画出它们的函数图象,通过看图,可以发现此不等式的解集是“xく-3或0くxく1” 用上面的知识解决问题:求不等式x
=x+2.然后求出它们的交点的坐标, 并在同一直角坐标系中画出它们的函数图象,通过看图,可以发现此不等式的解集是“xく-3或0くxく1” 用上面的知识解决问题:求不等式x -x>x+3的解集.
-x>x+3的解集. 
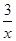 ﹥x+2的解集呢? 我们可以设
﹥x+2的解集呢? 我们可以设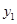 =
=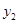 =x+2.然后求出它们的交点的坐标,
并在同一直角坐标系中画出它们的函数图象,通过看图,可以发现此不等式的解集是“xく-3或0くxく1” 用上面的知识解决问题:求不等式x
=x+2.然后求出它们的交点的坐标,
并在同一直角坐标系中画出它们的函数图象,通过看图,可以发现此不等式的解集是“xく-3或0くxく1” 用上面的知识解决问题:求不等式x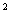 -x>x+3的解集.
-x>x+3的解集. 
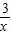 >x+2的解集呢我们可以设y1=
>x+2的解集呢我们可以设y1=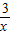 ,y2=x+2.然后求出它们的交点的坐标,并在同一直角坐标系中画出它们的函数图象,通过看图,可以发现此不等式的解集是“x<-3或0<x<1”
,y2=x+2.然后求出它们的交点的坐标,并在同一直角坐标系中画出它们的函数图象,通过看图,可以发现此不等式的解集是“x<-3或0<x<1”