题目内容
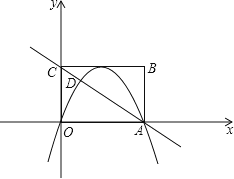
【题目】如图，在平面直角坐标系中，点
、
在函数
的图象上．当
时，过点P分别作x轴、y轴的垂线，垂足为点A、B；过点Q分别作x轴、y轴的垂线，垂足为点C、D．QD交PA于点E．随着m的增大，四边形ACQE的面积
A. 减小B. 增大C. 先减小后增大D. 先增大后减小
【答案】B
【解析】
首先利用m和n表示出AC和CQ的长，则四边形ACQE的面积即可利用m、n表示，然后根据函数的性质判断．
AC=m-1，CQ=n，
则S四边形ACQE=ACCQ=（m-1）n=mn-n．
∵P（1，4）、Q（m，n）在函数y=
（x＞0）的图象上，
∴mn=k=4（常数）．
∴S四边形ACQE=ACCQ=4-n，
∵当m＞1时，n随m的增大而减小，
∴S四边形ACQE=4-n随m的增大而增大．
故选B．
一线名师权威作业本系列答案【题目】9岁的小芳身高1.36米，她的表姐明年想报考北京的大学．表姐的父母打算今年暑假带着小芳及其表姐先去北京旅游一趟，对北京有所了解．他们四人7月31日下午从无锡出发，1日到4日在北京旅游，8月5日上午返回无锡．
无锡与北京之间的火车票和飞机票价如下：火车 (高铁二等座) 全票524元，身高1．1～1．5米的儿童享受半价票；飞机 (普通舱) 全票1240元，已满2周岁未满12周岁的儿童享受半价票．他们往北京的开支预计如下：
住宿费 (2人一间的标准间) | 伙食费 | 市内交通费 | 旅游景点门票费 （身高超过1.2米全票） |
每间每天x元 | 每人每天100元 | 每人每天y元 | 每人每天120元 |
假设他们四人在北京的住宿费刚好等于上表所示其他三项费用之和，7月31日和8月5日合计按一天计算，不参观景点，但产生住宿、伙食、市内交通三项费用．
（1）他们往返都坐火车，结算下来本次旅游总共开支了13668元，求x，y的值；
（2）若去时坐火车，回来坐飞机，且飞机成人票打五五折，其他开支不变，他们准备了14000元，是否够用? 如果不够，他们准备不再增加开支，而是压缩住宿的费用，请问他们预定的标准间房价每天不能超过多少元?
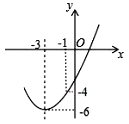
【题目】二次函数y=ax2+bx+c（a，b，c为常数，且a≠0）中的x与y的部分对应值如下表：
X | ﹣1 | 0 | 1 | 3 |
y | ﹣1 | 3 | 5 | 3 |
下列结论：
⑴ac＜0；
⑵当x＞1时，y的值随x值的增大而减小．
⑶3是方程ax2+（b﹣1）x+c=0的一个根；
⑷当﹣1＜x＜3时，ax2+（b﹣1）x+c＞0．
其中正确的个数为（）
A. 4个 B. 3个 C. 2个 D. 1个
【题目】越来越多的人在用微信付款、转帐.把微信账户里的钱转到银行卡叫做提现，自2016年3月1日起，每个微信账户终身享有1000元的免费提现额度，当累计提现金额超过1000元时，超出的部分需支付0.1%的手续费，以后每次提现支付的手续费均为提现金额的0.1%.
（1）小颖2018年开始使用微信，她用自己的微信账户第一次提现金额为1800元，需支付手续费多少元？
（2）小亮自2016年3月1日至今，用自己的微信账户共提现三次，提现金额和手续费如下：
第一次 | 第二次 | 第三次 | |
提现金额/元 |
|
|
|
手续费/元 | 0 | 0.4 | 3.4 |
求小亮前两次提现的金额分别为多少元.
【题目】九（1）班数学兴趣小组经过市场调查，整理出某种商品在第x（1≤x≤90）天的售价与销售量的相关信息如下表：
时间x（天） | 1≤x＜50 | 50≤x≤90 |
售价（元/件） | x+40 | 90 |
每天销量（件） | 200﹣2x | 200﹣2x |
已知该商品的进价为每件30元，设销售该商品的每天利润为y元
（1）求出y与x的函数关系式；
（2）问销售该商品第几天时，当天销售利润最大，最大利润是多少？
（3）该商品在销售过程中，共有多少天每天销售利润不低于4800元？请直接写出结果．