Question

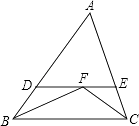
【题目】如图，在△ABC中，AB=AC，∠ABC=60°，D是三角形外一点，且BD=CD，AD与BC交于一点E，∠BDC=120°，则下列结论错误的是（ ）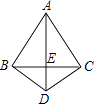
A.AD垂直平分BC
B.AB=2BD
C.∠ACD=90°
D.△ABD≌△ACD

Answer 1

【答案】B
【解析】解：∵AB=AC，BD=CD， ∴直线AD是线段BC的垂直平分线，
∴AD垂直平分BC，∴A符合题意；
∵∠ABC=60°，AB=AC，
∴△ABC是等边三角形，
∴∠BAC=60°，又∠BDC=120°，
∴∠ABC=∠ACD=90°，∴C符合题意；
∵∠ABC=60°，
∴∠BAD=30°，
∴AD=2BD，∴B不符合题意；
在△ABD和△ACD中，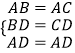
，
∴△ABD≌△ACD，∴D符合题意，
故选：B．
【考点精析】认真审题，首先需要了解线段垂直平分线的性质(垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线；线段垂直平分线的性质定理：线段垂直平分线上的点和这条线段两个端点的距离相等)．