题目内容
【题目】如图,△ABC中,∠ABC与∠ACB的平分线交于点F,过点F作DE∥BC交AB于点D,交AC于点E,那么下列结论: ①△BDF和△CEF都是等腰三角形;②DE=BD+CE;③△ADE的周长等于AB与AC的和;④BF=CF.其中正确的有 . (填正确的序号)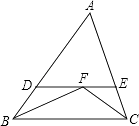
【答案】①②③
【解析】解:∵DE∥BC, ∴∠DFB=∠FBC,∠EFC=∠FCB,
∵△ABC中,∠ABC与∠ACB的平分线交于点F,
∴∠DBF=∠FBC,∠ECF=∠FCB,
∴∠DBF=∠DFB,∠ECF=∠EFC,
∴DB=DF,EF=EC,
即△BDF和△CEF都是等腰三角形;
故①正确;
∴DE=DF+EF=BD+CE,
故②正确;
∴△ADE的周长为:AD+DE+AE=AB+BD+CE+AE=AB+AC;
故③正确;
∵∠ABC不一定等于∠ACB,
∴∠FBC不一定等于∠FCB,
∴BF与CF不一定相等,
故④错误.
所以答案是:①②③.
【考点精析】关于本题考查的平行线的性质,需要了解两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补才能得出正确答案.

 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案【题目】一销售某品牌冰箱的公司有营销人员14人,销售部为制定销售人员月销售冰箱定额(单位:台),统计了14人某月的销售量如下表:
每人销售台数 | 20 | 17 | 13 | 8 | 5 | 4 |
人数 | 1 | 1 | 2 | 5 | 3 | 2 |
(1)这14位营销员该月销售冰箱的平均数、众数和中位数分别是多少?
(2)你认为销售部经理给这14位营销员定出每月销售冰箱的定额为多少台才比较合适?并说明理由.
【题目】为响应市教育局倡导的“阳光体育运动”的号召,全校学生积极参与体育运动.为了进一步了解学校九年级学生的身体素质情况,体育老师在九年级800名学生中随机抽取50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图,如下所示:
组别 | 次数x | 频数(人数) |
第1组 | 80≤x<100 | 6 |
第2组 | 100≤x<120 | 8 |
第3组 | 120≤x<140 | a |
第4组 | 140≤x<160 | 18 |
第5组 | 160≤x<180 | 6 |
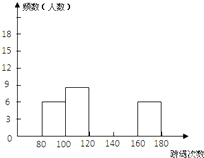
请结合图表完成下列问题:
(1)表中的a=;
(2)请把频数分布直方图补充完整;
(3)这个样本数据的中位数落在第组;
(4)若九年级学生一分钟跳绳次数(x)达标要求是:x<120为不合格;120≤x<140为合格;140≤x<160为良;x≥160为优.根据以上信息,请你估算学校九年级同学一分钟跳绳次数为优的人数为 .