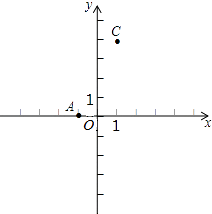题目内容
【题目】如图,方格纸中的每个小方格都是边长为1的正方形,我们把以格点间连线为边的三角形称为“格点三角形”,图中的△ABC就是格点三角形,建立如图所示的平面直角坐标系,点C的坐标为(0,﹣1).
(1)在如图的方格纸中把△ABC以点O为位似中心扩大,使放大前后的位似比为1:2,画出△A1B2C2(△ABC与△A1B2C2在位似中心O点的两侧,A,B,C的对应点分别是A1 , B2 , C2).
(2)利用方格纸标出△A1B2C2外接圆的圆心P,P点坐标是⊙P的半径= . (保留根号)
【答案】
(1)
解:如图,△A1B2C2为所作

(2)(3,1);![]()
【解析】解: (2)点P的坐标为(3,1),
PA1= ![]() =
= ![]() ,
,
即⊙P的半径为 ![]() .
.
故答案为(3,1), ![]() .
.
(1)利用关于原点为位似中心的两图形的对应的坐标关系写出点A1 , B2 , C2的坐标,然后描点即可得到△A1B2C2;(2)利用网格特点,作A1C2和C2B2的垂值平分线得到△A1B2C2外接圆的圆心P,然后写出P点坐标和计算PA1 .

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
相关题目