题目内容
【题目】如图,已知正方形ABCD,点E是边AB上一点,点O是线段AE上的一个动点(不与A、E重合),以O为圆心,OB为半径的圆与边AD相交于点M,过点M作⊙O的切线交DC于点N,连结OM、ON、BM、BN.
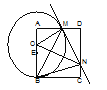
求证:(1)△AOM∽△DMN; (2)求∠MBN的度数.
【答案】(1)、证明过程见解析;(2)、45°.
【解析】试题分析:(1)、根据切成的性质得出∠AMO+∠DMN=90°,根据正方形性质得出∠A=∠D=90°,即∠AMO+∠AOM=90°,从而得出∠AOM=∠DMN,得出三角形相似;(2)、作BP⊥MN,根据切线和AD∥BC得出Rt△MAB≌Rt△MPB,得到∠ABM=∠MBP,BP=AB=BC,然后得出Rt△BPN≌Rt△BCN,得出∠PBN=∠CBN,根据∠MBN=∠MBP+∠PBN=![]() ∠ABC得出答案.
∠ABC得出答案.
试题解析:(1)、∵MN是⊙O的切线, ∴OM⊥MN,∴∠AMO+∠DMN=90°,
又∵四边形ABCD为正方形, ∴∠A=∠D=90°,∴∠AMO+∠AOM=90°, ∴∠AOM=∠DMN,
∴△AMO∽△DMN
(2)、如图,作BP⊥MN于点P,

∵MN是⊙O的切线,∴∠PMB+∠BMO=90°,
∵∠ABC=90°,∴∠CBM+∠MBO=90°, ∵OB=OM,∴∠BMO=∠MBO, ∴∠PMB=∠CBM,
∵AD∥BC,∴∠CBM=∠AMB, ∴∠AMB=∠PMB,
在Rt△MAB和Rt△MPB中, , ∴Rt△MAB≌Rt△MPB(AAS)
, ∴Rt△MAB≌Rt△MPB(AAS)
∴∠ABM=∠MBP,BP=AB=BC,
在Rt△BPN和Rt△BCN中,![]() , ∴Rt△BPN≌Rt△BCN(HL) ∴∠PBN=∠CBN,
, ∴Rt△BPN≌Rt△BCN(HL) ∴∠PBN=∠CBN,
∴∠MBN=∠MBP+∠PBN=![]() ∠ABC=45°.
∠ABC=45°.

练习册系列答案
相关题目