题目内容
【题目】我们知道，任意一个正整数n都可以进行这样的分解：
（p，q是正整数，且
），在n的所有这种分解中，如果p，q两因数之差的绝对值最小，我们就称p×q是n的完美分解．并规定：
．
例如18可以分解成1×18，2×9或3×6，因为18－1＞9－2＞6－3，所以3×6是18的完美分解，所以F（18）＝
．
（1）F（13）＝ ，F（24）＝ ；
（2）如果一个两位正整数t，其个位数字是a，十位数字为
，交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为36，那么我们称这个数为“和谐数”，求所有“和谐数”；
（3）在（2）所得“和谐数”中，求F（t）的最大值．
【答案】（1）
，
（2）所以和谐数为15，26，37，48，59；（3）F（t）的最大值是
．
【解析】
(1)根据题意,按照新定义的法则计算即可.
(2)根据新定义的”和谐数”定义,将数用a,b表示列出式子解出即可.
(3)根据(2)中计算的结果求出最大即可.
解：（1）F（13）＝，F（24）＝;
（2）原两位数可表示为
新两位数可表示为
∴
∴
∴
∴
∴
（
且b为正整数 ）
∴b=2,a=5; b=3,a=6, b=4,a=7,
b=5,a=8 b=6,a=9
所以和谐数为15，26，37，48，59
(3)所有“和谐数”中，F（t）的最大值是．
练习册系列答案
相关题目
【题目】张明、王成两位同学在初二学年10次数学单元检测的成绩（成绩均为整数，且个位数为0）如图所示利用图中提供的信息，解答下列问题：
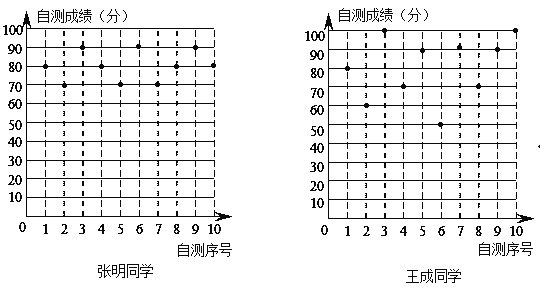
（1）完成下表：
姓名 | 平均成绩 | 中位数 | 众数 | 方差（s2） |
张明 |
| 80 | 80 |
|
王成 |
|
|
| 260 |
（2）如果将90分以上（含90分）的成绩视为优秀，则优秀率较高的同学是 ；
（3）根据图表信息，请你对这两位同学各提出学习建议．
