Question

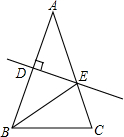如图，等腰△ABC的周长为27，底边BC=5，AB的垂直平分线DE交AB于点D，交AC于点E，则△BEC的周长为（　　）

A．13

B．14

C．15

D．16

Answer 1

分析：由三角形ABC的周长与底边求出腰长，由AB的垂直平分线DE，利用线段垂直平分线的性质得到AE=BE，三角形BEC的周长为BE+EC+BC，等量代换得到AC+BC，求出即可．

解答：解：∵DE垂直平分AB，
∴AE=BE，
∵等腰△ABC的周长为27，底边BC=5，
∴AB=AC=

27-5

2

=11，
则△BEC周长为BE+EC+BC=AE+EC+BC=AC+BC=11+5=16．
故选D

点评：此题考查了线段垂直平分线性质，以及等腰三角形的性质，熟练掌握线段垂直平分线的性质是解本题的关键．