��Ŀ����
����Ŀ����֪��ABC�ǵ��������Σ���BAC=90����CD=![]() BC��DE��CE��DE=CE������AE����M��AE���е�.
BC��DE��CE��DE=CE������AE����M��AE���е�.
��1����ͼ1������D��BC���ϣ�����CM����AB=4ʱ����CM�ij���
��2����ͼ2������D����ABC���ڲ�������BD����N��BD�е㣬����MN��NE����֤MN��AE��
��3����ͼ3����ͼ2�е���CDE�Ƶ�C��ʱ����ת��ʹ��BCD=30��������BD����N��BD�е㣬����MN��̽��![]() ��ֵ��ֱ��д�����
��ֵ��ֱ��д�����

���𰸡���1��![]() ����2��֤�����̼���������3��
����2��֤�����̼���������3��![]() .
.
��������
�����������1�����ݵ���ֱ��������ABC�ó�BC�ij��ȣ�Ȼ����ݵ���ֱ��������DCE�ó�CE�ij��ȣ�Ȼ�����Rt��ACE�Ĺ��ɶ����ó�AE�ij��ȣ��Ӷ�����ֱ��������б���ϵ����ߵ���б�ߵ�һ��ó��𰸣���2���ӳ�EN��NF��ʹNE=NF��������BF��AF��Ȼ��֤����ABF�ա�ACE���Ӷ��ó���FAE=��BAC=90����Ȼ�����ƽ���ߵ����ʵó��𰸣���3�����ݵڶ���ͬ���ķ����ó�MN=![]() AF��AF=AE���Ӷ��ó���.
AF��AF=AE���Ӷ��ó���.
�����������1����AB=AC=4 ��BAC=90�� ��BC=4![]() ��CD=2
��CD=2![]() ��CE=2��
��CE=2��
����Rt��ACE�Ĺ��ɶ����ɵã�AE=![]() ��CM=
��CM=![]()
��2����ͼ���ӳ�EN��NF��ʹNE=NF��������BF��AF��
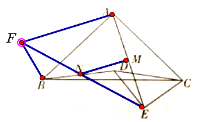
�ɵ�BF=DE=CE����FBN=��NDE�� ����ACE=90��-��DCB
��ABF=��BDE-��ABN=��180��-��DBC-��DCB-��EDC-��ABN=180��-����DBC+��ABN��-45��-��DCB=90��-��DCB
������ACE=��ABF��������ABF�ա�ACE�� ������FAB=��EAC�� ������FAE=��BAC=90����
��ΪMN//AF������MN��AE��
��3��ͬ��2���ɵ�MN=![]() AF��AF=AE��
AF��AF=AE��
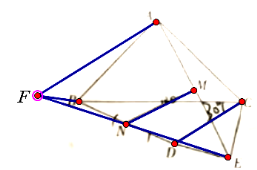
��AC=2CE����ACE=120���������AE=![]() �� ����
�� ����![]()
