Question

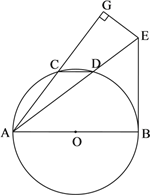
【题目】如图，AB是⊙O的直径，CD为⊙O 的弦，过点B作⊙O的切线，交AD的延长线于点E，连接AC并延长，过点E作EG⊥AC的延长线于点G，并且∠GCD= ∠GAB.

（1）求证： ；

（2）若AB=10，sin∠ADC=，求AG的长．

Answer 1

【答案】（1）证明见解析；（2）12

【解析】（1）证明：∵∠GCD= ∠GAB,∴CD∥AB.

∴∠CDA= ∠DAB.∴.

（2）连接BC，交AE于点M.

∵ AB是⊙O直径，∴∠ACB = 90°．

∵EG⊥AC的延长线于点G,

∴∠EGA = 90°．∴CM∥EG.

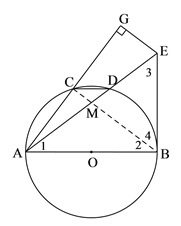
∵ BE是⊙O的切线, ∴BE⊥AB于点B.

∵,∴ ∠1= ∠2．∴AM=BM.

∵∠1+∠3= ∠2+∠4,

∴ ∠3= ∠4．∴ BM= EM．∴AM=EM.∴M是AE的中点.

∵CM∥EG,∴C是AG的中点.∴AC=CG.

∵sin∠ADC=，∴sin∠ABC=.

在Rt△ABC中，sin∠ABC=，AB=10.

∴ AC=6．∴CG.=6. ∴AG.=12.