جâؤ؟ؤعبف
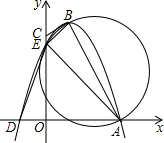 £¨2013•زث³اتذؤ£ؤ⣩بçح¼£¬ثؤ±كذخOABCµؤ±كOA،¢OC·ض±ًشعxضل،¢yضلµؤص°ëضلةد£¬¶¥µمشعBµمµؤإ×خïدك½»xضلسعµمA،¢D£¬½»yضلسعµمE£¬ء¬½سAE،¢BE£®زرضھtan،دCBE=
£¨2013•زث³اتذؤ£ؤ⣩بçح¼£¬ثؤ±كذخOABCµؤ±كOA،¢OC·ض±ًشعxضل،¢yضلµؤص°ëضلةد£¬¶¥µمشعBµمµؤإ×خïدك½»xضلسعµمA،¢D£¬½»yضلسعµمE£¬ء¬½سAE،¢BE£®زرضھtan،دCBE=| 1 | 3 |
£¨1£©اَإ×خïدكµؤ½âخِت½¼°¶¥µمBµؤ×ّ±ê£»
£¨2£©اَض¤£؛CBتا،÷ABEحâ½سش²µؤاذدك£»
£¨3£©تشج½¾؟شعإ×خïدكةدتا·ٌ´وشعز»µمP£¬ت¹زشD،¢E،¢A،¢Pخھ¶¥µمµؤثؤ±كذختاجفذخ£؟بô´وشع£¬ض±½سذ´³ِµمPµؤ×ّ±ê£»بô²»´وشع£¬اëثµأ÷ہيسة£®
·ضخِ£؛£¨1£©ةèإ×خïدك½âخِت½خھy=ax2+bx+c½«A£¨3£¬0£©£¬D£¨-1£¬0£©£¬E£¨0£¬3£©´ْبë¼´؟ةµأ³ِa£¬b£¬cµؤضµ£¬½ّ¶ّµأ³ِإ×خïدكµؤ½âخِت½£»
£¨2£©¹µمB×÷BM،حyسعµمM£¬شٍM£¨0£¬4£©£®شعRt،÷AOEضذ£¬زٍخھOA=OE=3£¬ثùزش،د1=،د2=45،م£¬شظ¸ù¾ف¹´¹ة¶¨ہي¼´؟ةاَ³ِAEµؤ³¤£¬ح¬ہي؟ةµأ³ِBEµؤ³¤£¬
£¨3£©سةسعجفذخµؤء½µ×±ك²»ؤـب·¶¨£¬¹تس¦·ضEP،خAD£¬AE،خDP£¬DE،خAPبضضاé؟ِ½ّذذ·ضہàجضآغ£®
£¨2£©¹µمB×÷BM،حyسعµمM£¬شٍM£¨0£¬4£©£®شعRt،÷AOEضذ£¬زٍخھOA=OE=3£¬ثùزش،د1=،د2=45،م£¬شظ¸ù¾ف¹´¹ة¶¨ہي¼´؟ةاَ³ِAEµؤ³¤£¬ح¬ہي؟ةµأ³ِBEµؤ³¤£¬
£¨3£©سةسعجفذخµؤء½µ×±ك²»ؤـب·¶¨£¬¹تس¦·ضEP،خAD£¬AE،خDP£¬DE،خAPبضضاé؟ِ½ّذذ·ضہàجضآغ£®
½â´ً£؛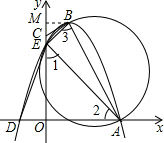 ½â£؛£¨1£©ةèإ×خïدك½âخِت½خھy=ax2+bx+c
½â£؛£¨1£©ةèإ×خïدك½âخِت½خھy=ax2+bx+c
½«A£¨3£¬0£©£¬D£¨-1£¬0£©£¬E£¨0£¬3£©´ْبëةدت½£¬µأ
£¬
½âµأ£؛a=-1£¬b=2£¬c=3£¬
،àإ×خïدكµؤ½âخِت½خھy=-x2+2x+3£®
سض،كy=-x2+2x+3=-£¨x-1£©2+4£¬
،àµمB£¨1£¬4£©£»
£¨2£©ض¤أ÷£؛بçح¼£¬¹µمB×÷BM،حyسعµمM£¬شٍM£¨0£¬4£©£®
شعRt،÷AOEضذ£¬
،كOA=OE=3£¬
،à،د1=،د2=45،م£¬AE=
=
=3
£®
شعRt،÷EMBضذ£¬EM=OM-OE=1=BM£¬
،à،دMEB=،دMBE=45،م£¬BE=
=
£®
،à،دBEA=180،م-،د1-،دMEB=90،م£®
،àABتا،÷ABEحâ½سش²µؤض±¾¶£®
شعRt،÷ABEضذ£¬tan،دBAE=
=
=tan،دCBE£¬
،à،دBAE=،دCBE£®
شعRt،÷ABEضذ£¬،دBAE+،د3=90،م£¬
،à،دCBE+،د3=90،م
،à،دCBA=90،م£¬¼´CB،حAB£®
،àCBتا،÷ABEحâ½سش²µؤاذدك£»
£¨3£©´وشع£®
µ±EP،خADت±£¬
،كE£¨0£¬3£©£¬
،àض±دكEPµؤ½âخِت½خھy=3£¬
،à
£¬½âµأ
£»
µ±AE،خDPت±£¬
ةèض±دكAEµؤ½âخِت½خھy=kx+b£¨k،ظ0£©£¬
،كA£¨3£¬0£©£¬E£¨0£¬3£©£¬
،à
£¬½âµأ
£¬
،àض±دكAEµؤ½âخِت½خھy=-x+3£¬
ةèض±دكDPµؤ½âخِت½خھy=-x+b£¬
،كD£¨-1£¬0£©£¬
،à1+b=0£¬½âµأb=-1£¬
،àض±دكDPµؤ½âخِت½خھy=-x-1£¬
،à
£¬½âµأ
»ٍ
£¨ةلب¥£©£¬
،àP£¨4£¬-5£©£»
µ±DE،خAPت±£¬
ةèض±دكDEµؤ½âخِت½خھy=kx+b£¨k،ظ0£©£¬
،كD£¨-1£¬0£©£¬E£¨0£¬3£©£¬
،à
£¬½âµأ
£¬
،àض±دكDEµؤ½âخِت½خھy=3x+3£¬
ةèض±دكAPµؤ½âخِت½خھy=3x+b£¬
،كA£¨3£¬0£©£¬
،à9+b=0£¬½âµأb=-9£¬
،àض±دكAPµؤ½âخِت½خھy=3x-9£¬
،à
£¬½âµأ
»ٍ
£¨ةلب¥£©£®
×غةدثùتِ£¬µمPµؤ×ّ±êخھ£¨2£¬3£©»ٍ£¨4£¬-5£©»ٍ£¨-4£¬-21£©£®
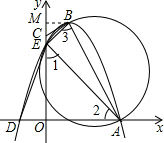 ½â£؛£¨1£©ةèإ×خïدك½âخِت½خھy=ax2+bx+c
½â£؛£¨1£©ةèإ×خïدك½âخِت½خھy=ax2+bx+c½«A£¨3£¬0£©£¬D£¨-1£¬0£©£¬E£¨0£¬3£©´ْبëةدت½£¬µأ
|
½âµأ£؛a=-1£¬b=2£¬c=3£¬
،àإ×خïدكµؤ½âخِت½خھy=-x2+2x+3£®
سض،كy=-x2+2x+3=-£¨x-1£©2+4£¬
،àµمB£¨1£¬4£©£»
£¨2£©ض¤أ÷£؛بçح¼£¬¹µمB×÷BM،حyسعµمM£¬شٍM£¨0£¬4£©£®
شعRt،÷AOEضذ£¬
،كOA=OE=3£¬
،à،د1=،د2=45،م£¬AE=
| OA2+OE2 |
| 32+32 |
| 2 |
شعRt،÷EMBضذ£¬EM=OM-OE=1=BM£¬
،à،دMEB=،دMBE=45،م£¬BE=
| EM2+BM2 |
| 2 |
،à،دBEA=180،م-،د1-،دMEB=90،م£®
،àABتا،÷ABEحâ½سش²µؤض±¾¶£®
شعRt،÷ABEضذ£¬tan،دBAE=
| BE |
| AE |
| 1 |
| 3 |
،à،دBAE=،دCBE£®
شعRt،÷ABEضذ£¬،دBAE+،د3=90،م£¬
،à،دCBE+،د3=90،م
،à،دCBA=90،م£¬¼´CB،حAB£®
،àCBتا،÷ABEحâ½سش²µؤاذدك£»
£¨3£©´وشع£®
µ±EP،خADت±£¬
،كE£¨0£¬3£©£¬
،àض±دكEPµؤ½âخِت½خھy=3£¬
،à
|
|
µ±AE،خDPت±£¬
ةèض±دكAEµؤ½âخِت½خھy=kx+b£¨k،ظ0£©£¬
،كA£¨3£¬0£©£¬E£¨0£¬3£©£¬
،à
|
|
،àض±دكAEµؤ½âخِت½خھy=-x+3£¬
ةèض±دكDPµؤ½âخِت½خھy=-x+b£¬
،كD£¨-1£¬0£©£¬
،à1+b=0£¬½âµأb=-1£¬
،àض±دكDPµؤ½âخِت½خھy=-x-1£¬
،à
|
|
|
،àP£¨4£¬-5£©£»
µ±DE،خAPت±£¬
ةèض±دكDEµؤ½âخِت½خھy=kx+b£¨k،ظ0£©£¬
،كD£¨-1£¬0£©£¬E£¨0£¬3£©£¬
،à
|
|
،àض±دكDEµؤ½âخِت½خھy=3x+3£¬
ةèض±دكAPµؤ½âخِت½خھy=3x+b£¬
،كA£¨3£¬0£©£¬
،à9+b=0£¬½âµأb=-9£¬
،àض±دكAPµؤ½âخِت½خھy=3x-9£¬
،à
|
|
|
×غةدثùتِ£¬µمPµؤ×ّ±êخھ£¨2£¬3£©»ٍ£¨4£¬-5£©»ٍ£¨-4£¬-21£©£®
µمئہ£؛±¾جâ؟¼²éµؤتا¶´خ؛¯ت×غ؛دج⣬ةو¼°µ½سأ´¶¨دµت·¨اَ¶´خ؛¯ت¼°ز»´خ؛¯تµؤ½âخِت½£¬ء½ض±دكئ½ذذµؤدà¹طضھت¶£¬ؤر¶بتتضذ£®

ء·د°²لدµءذ´ً°¸
 جىجىدٍةدز»±¾؛أ¾يدµءذ´ً°¸
جىجىدٍةدز»±¾؛أ¾يدµءذ´ً°¸ ذ،ر§ةْ10·ضضسس¦سأجâدµءذ´ً°¸
ذ،ر§ةْ10·ضضسس¦سأجâدµءذ´ً°¸
دà¹طجâؤ؟