题目内容
已知关于x的一元二次方程:x2-2(-a+1)x+a2-1=0有两个不相等的实数根x1,x2;且有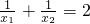 ,求a的值及方程两根x1,x2.
,求a的值及方程两根x1,x2.
解:∵一元二次方程:x2-2(-a+1)x+a2-1=0有两个不相等的实数根x1,x2,
∴△=4(-a+1)2-4(a2-1)>0,解得a<1;
∴ ,
,
由③得, =2,把①②代入得,
=2,把①②代入得, =2,
=2,
解得a=-2或a=1(舍去).
当x=-2时原方程可化为x2-6x+3=0,
解得x1=3+ ,x2=3-
,x2=3- .
.
分析:先根据方程有两个不相等的实数根得到△=4(-a+1)2-4(a2-1)>0,求出a的取值范围,然后根据根与系数的关系得到x1+x2=2(-a+1),x1•x2=a2-1与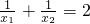 组成方程组,求出a的值及方程两根x1,x2.
组成方程组,求出a的值及方程两根x1,x2.
点评:本题考查的是一元二次方程根与系数的关系及根的判别式,先判断出a的取值范围,再由根与系数的关系得出方程组是解答此题的关键.
∴△=4(-a+1)2-4(a2-1)>0,解得a<1;
∴
 ,
,由③得,
 =2,把①②代入得,
=2,把①②代入得, =2,
=2,解得a=-2或a=1(舍去).
当x=-2时原方程可化为x2-6x+3=0,
解得x1=3+
 ,x2=3-
,x2=3- .
.分析:先根据方程有两个不相等的实数根得到△=4(-a+1)2-4(a2-1)>0,求出a的取值范围,然后根据根与系数的关系得到x1+x2=2(-a+1),x1•x2=a2-1与
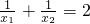 组成方程组,求出a的值及方程两根x1,x2.
组成方程组,求出a的值及方程两根x1,x2.点评:本题考查的是一元二次方程根与系数的关系及根的判别式,先判断出a的取值范围,再由根与系数的关系得出方程组是解答此题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
已知关于x的一元二次x2-6x+k+1=0的两个实数根x1,x2,
+
=1,则k的值是( )
| 1 |
| x1 |
| 1 |
| x2 |
| A、8 | B、-7 | C、6 | D、5 |
 .
. .
.