题目内容
【题目】如图,在四边形BCED中,∠D=E=90°,A是DE上一点,且AB⊥AC,,AB=AC,若BD=4cm,CE=3cm, (1)说明DE、BD、EC三者之间存在怎样的数量关系?(2)求![]() 的面积。
的面积。

【答案】(1)DE=BD+CE,理由见解析;(2)12.5
【解析】试题分析:(1)根据AAS得到△ABD≌△CAE,得出AD=EC,BD=AE,从而推出DE=BD+CE;
(2)根据勾股定理求得AB的长度,再求三角形的面积.
试题解析:
∵∠D=90°,
∴∠DBA+∠BAD=90°,
又∵AB⊥AC,
∴∠BAD+∠CAE=90°,
∴∠DBA=∠CAE(同角的余角相等),
在△DBA和△EAC中
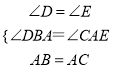 ,
,
∴△DBA≌△EAC(AAS),
∴AD=EC,BD=AE,
又∵DE=DA+AE,
∴DE=BD+CE;
(2)∵AD=EC,CE=3cm,
∴AD=3,
在Rt△ABD中,BD=4cm,
∴AB=![]() cm,
cm,
又∵AB=AC,
∴AC=5cm,
∴S△ABC=![]() cm2.
cm2.

练习册系列答案
相关题目
