题目内容
【题目】(阅读材料)
我们知道“在数轴上表示的两个数,右边的数总比左边的数大”,利用此规律,我们可以求数轴上两个点之间的距离,具体方法是:用右边的数减去左边的数的差就是表示这两个数的两点之间的距离.若点![]() 表示的数是
表示的数是![]() ,点
,点![]() 表示的数是
表示的数是![]() ,点
,点![]() 在点
在点![]() 的右边(即
的右边(即![]() ),则点
),则点![]() ,
,![]() 之间的距离为
之间的距离为![]() (即
(即![]() ).
).
例如:若点![]() 表示的数是-6,点
表示的数是-6,点![]() 表示的数是-9,则线段
表示的数是-9,则线段![]() .
.
(理解应用)
(1)已知在数轴上,点![]() 表示的数是-2020,点
表示的数是-2020,点![]() 表示的数是2020,求线段
表示的数是2020,求线段![]() 的长;
的长;
(拓展应用)
如图,数轴上有三个点,点![]() 表示的数是-2,点
表示的数是-2,点![]() 表示的数是3,点
表示的数是3,点![]() 表示的数是
表示的数是![]() .
.
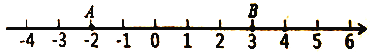
(2)当![]() ,
,![]() ,
,![]() 三个点中,其中一个点是另外两个点所连线段的中点时,求
三个点中,其中一个点是另外两个点所连线段的中点时,求![]() 的值;
的值;
(3)在点![]() 左侧是否存在一点
左侧是否存在一点![]() ,使点
,使点![]() 到点
到点![]() ,点
,点![]() 的距离和为19?若存在,求出点
的距离和为19?若存在,求出点![]() 表示的数:若不存在,请说明理由.
表示的数:若不存在,请说明理由.
【答案】(1)4040;(2)0.5,7或8;(3)-9.
【解析】
(1)根据题意,用点![]() 表示的数减去点
表示的数减去点![]() 表示的数加以计算即可;
表示的数加以计算即可;
(2)根据题意分①点![]() 是线段
是线段![]() 的中点、②点
的中点、②点![]() 是线段
是线段![]() 的中点、③点
的中点、③点![]() 是线段
是线段![]() 的中点三种情况进一步分析讨论即可;
的中点三种情况进一步分析讨论即可;
(3)设点![]() 表示的数是
表示的数是![]() ,然后分别表示出AQ与BQ,根据“点
,然后分别表示出AQ与BQ,根据“点![]() 到点
到点![]() ,点
,点![]() 的距离和为19”进一步求解即可.
的距离和为19”进一步求解即可.
(1)![]() ;
;
(2)①当点![]() 是线段
是线段![]() 的中点时,则
的中点时,则![]() .
.
所以![]() .解得:
.解得:![]() ;
;
②当点![]() 是线段
是线段![]() 的中点时,则
的中点时,则![]() .
.
所以![]() .解得:
.解得:![]() ;
;
③当点![]() 是线段
是线段![]() 的中点时,则
的中点时,则![]() .
.
所以![]() .解得:
.解得:![]() ;
;
综上所述,![]() 的值为0.5、
的值为0.5、![]() 或8;
或8;
(3)设点![]() 表示的数是
表示的数是![]() ,则:QA=
,则:QA=![]() ,QB=
,QB=![]() ,
,
∵![]() ,
,
∴![]() .
.
解得:![]() .
.
∴在点![]() 左侧存在一点
左侧存在一点![]() ,使点
,使点![]() 到点
到点![]() ,
,![]() 的距离和为19.且点
的距离和为19.且点![]() 表示的数是-9.
表示的数是-9.

【题目】某商场购进了一批![]() 、
、![]() 两种型号的智能扫地机器人,这两种智能扫地机器人的进购数量、进价、售价如表所示:
两种型号的智能扫地机器人,这两种智能扫地机器人的进购数量、进价、售价如表所示:
类型 | 进购数量(个) | 进价(元/个) | 售价(元/个) |
| 20 | 1800 | 2300 |
| 40 | 1500 | ? |
若该商场计划全部销售完这批智能扫地机器人的总利润不少于32000元,则![]() 型智能扫地机器人的销售单价至少是多少元?
型智能扫地机器人的销售单价至少是多少元?