题目内容
(2012•长春一模)如图,点A、B分别为抛物线y=-
x2+bx+4、y=
x2-2x+c与y轴交点,两条抛物线都经过点C(6,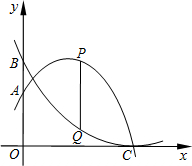 0).点P、Q分别在抛物线y=-
0).点P、Q分别在抛物线y=-
x2+bx+4、y=
x2-2x+c上,点P在点Q的上方,PQ平行y轴.设点P的横坐标为m.
(1)求b和c的值.
(2)求以A、B、P、Q为顶点的四边形是平行四边形时m的值.
(3)当m为何值时,线段PQ的长度取得最大值?并求出这个最大值.
(4)直接写出线段PQ的长度随m增大而减小的m的取值范围.
| 1 |
| 3 |
| 1 |
| 6 |
 0).点P、Q分别在抛物线y=-
0).点P、Q分别在抛物线y=-| 1 |
| 3 |
| 1 |
| 6 |
(1)求b和c的值.
(2)求以A、B、P、Q为顶点的四边形是平行四边形时m的值.
(3)当m为何值时,线段PQ的长度取得最大值?并求出这个最大值.
(4)直接写出线段PQ的长度随m增大而减小的m的取值范围.
分析:(1)把点C的坐标代入两抛物线解析式,计算即可求出b、c的值;
(2)求出A、B的坐标,然后求出AB的长度,再根据点P的横坐标利用抛物线解析式表示出点P、Q的坐标,然后表示出PQ的长度,根据平行四边形的对边平行且相等列出方程,然后求解即可得到m的值;
(3)根据线段PQ的表达式转化为顶点式解析式,再利用二次函数的最值问题解答即可;
(4)根据PQ的表达式的顶点式形式,利用二次函数的增减性解答即可.
(2)求出A、B的坐标,然后求出AB的长度,再根据点P的横坐标利用抛物线解析式表示出点P、Q的坐标,然后表示出PQ的长度,根据平行四边形的对边平行且相等列出方程,然后求解即可得到m的值;
(3)根据线段PQ的表达式转化为顶点式解析式,再利用二次函数的最值问题解答即可;
(4)根据PQ的表达式的顶点式形式,利用二次函数的增减性解答即可.
解答:解:(1)∵两条抛物线都经过点C(6,0),
∴-
×62+6b+4=0,
解得b=
,
×62-2×6+c=0,
解得c=6;
(2)根据题意,点A的坐标为(0,4),点B的坐标为(0,6),
所以,AB=2,
∵点P的横坐标为m,
∴P(m,-
m2+
m+4),
∵PQ∥y轴,
∴点Q(m,
m2-2m+6),
∴PQ=(-
m2+
m+4)-(
m2-2m+6)=-
m2+
m+4-
m2+2m+6=-
m2+
m-2,
∴当PQ=AB时,-
m2+
m-2=2,
整理得,3m2-20m+24=0,
解得m1=
,m2=
,
故以A、B、P、Q为顶点的四边形是平行四边形时,m的值为
或
;
(3)由(2)知,PQ=-
m2+
m-2=-
(m-
)2+
,
所以,当m=
时,线段PQ的长度最大,线段PQ的最大长度为
;
(4)由(3)知,PQ=-
(m-
)2+
,
所以,线段PQ的长度随m增大而减小的m的取值范围是
≤m<6.
∴-
| 1 |
| 3 |
解得b=
| 4 |
| 3 |
| 1 |
| 6 |
解得c=6;
(2)根据题意,点A的坐标为(0,4),点B的坐标为(0,6),
所以,AB=2,
∵点P的横坐标为m,
∴P(m,-
| 1 |
| 3 |
| 4 |
| 3 |
∵PQ∥y轴,
∴点Q(m,
| 1 |
| 6 |
∴PQ=(-
| 1 |
| 3 |
| 4 |
| 3 |
| 1 |
| 6 |
| 1 |
| 3 |
| 4 |
| 3 |
| 1 |
| 6 |
| 1 |
| 2 |
| 10 |
| 3 |
∴当PQ=AB时,-
| 1 |
| 2 |
| 10 |
| 3 |
整理得,3m2-20m+24=0,
解得m1=
10+2
| ||
| 3 |
10-2
| ||
| 3 |
故以A、B、P、Q为顶点的四边形是平行四边形时,m的值为
10+2
| ||
| 3 |
10-2
| ||
| 3 |
(3)由(2)知,PQ=-
| 1 |
| 2 |
| 10 |
| 3 |
| 1 |
| 2 |
| 10 |
| 3 |
| 32 |
| 9 |
所以,当m=
| 10 |
| 3 |
| 32 |
| 9 |
(4)由(3)知,PQ=-
| 1 |
| 2 |
| 10 |
| 3 |
| 32 |
| 9 |
所以,线段PQ的长度随m增大而减小的m的取值范围是
| 10 |
| 3 |
点评:本题考查了二次函数的综合题型,主要利用了待定系数法求二次函数解析式,平行四边形的对边平行且相等的性质,二次函数的最值问题,二次函数的增减性,综合性较强,但难度不大,把点C的坐标代入函数解析式求出b、c的值是解题的关键,也是本题的突破口.

练习册系列答案
相关题目
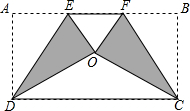 (2012•长春一模)将矩形纸片ABCD按如图方式折叠,DE、CF为折痕,折叠后点A和点B都落在点O处.若△EOF是等边三角形,则
(2012•长春一模)将矩形纸片ABCD按如图方式折叠,DE、CF为折痕,折叠后点A和点B都落在点O处.若△EOF是等边三角形,则 (2012•长春一模)如图,抛物线y=ax2-x-
(2012•长春一模)如图,抛物线y=ax2-x- -B于点P,以PQ为一边向右作正方形PQRS,设运动时间为t(秒),正方形PQRS与梯形OABC重叠面积为S(平方单位)
-B于点P,以PQ为一边向右作正方形PQRS,设运动时间为t(秒),正方形PQRS与梯形OABC重叠面积为S(平方单位)