题目内容

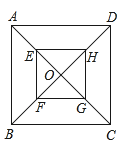
【题目】如图所示，正方形EFGH是由正方形ABCD经过位似变换得到的，点O是位似中心，E，F，G，H分别是OA，OB，OC，OD的中点，则正方形EFGH与正方形ABCD的面积比是（　　）

A. 1：6B. 1：5C. 1：4D. 1：2

【答案】C

【解析】

由正方形EFGH是由正方形ABCD经过位似变换得到的，点O是位似中心，E，F，G，H分别是OA，OB，OC，OD的中点，易求得位似比等于EH：AD=1：2，又由相似三角形面积的比等于相似比的平方，即可求得正方形EFGH与正方形ABCD的面积比．

∵正方形EFGH是由正方形ABCD经过位似变换得到的，点O是位似中心，

∴正方形EFGH∽正方形ABCD，

∵E，F，G，H分别是OA，OB，OC，OD的中点，

∴EH=AD，

即位似比为：EH：AD=1：2，

∴正方形EFGH与正方形ABCD的面积比是：1：4．

故选C．

练习册系列答案
相关题目

【题目】如图，是ABC的外接圆，AB为直径，∠BAC的平分线交于点D，过点D作DEAC分别交AC、AB的延长线于点E、F．

（1）求证：EF是的切线；

（2）若AC=4，CE=2，求的长度．（结果保留）

【题目】二次函数y＝ax2+bx+c（a≠0，a，b，c为常数）图象如图所示，根据图象解答问题．

（1）写出过程ax2+bx+c＝0的两个根．

（2）写出不等式ax2+bx+c＞0的解集．

（3）若方程ax2+bx+c＝k有两个不相等的实数根，求k的取值范围．

【题目】已知在图（1）与图（2）中，每个小方格都是边长为1个单位的正方形，△AOB的三个顶点都在格点上．

（1）将△OAB关于点P对称，在图（1）中画出对称后的图形△O′A′B′，并涂黑；

（2）先画出△OAB关于y轴的轴对称图形△O′A′B′，然后将△O′A′B′向右平移2个单位，再向上平移3个单位，在图（2）中画出平移后的图形△O″A″B″，并涂黑．

【题目】已知二次函数y=x2﹣x+m的图象经过点A(1，﹣2)

(1)求此函数图像与坐标轴的交点坐标；

(2)若P(-2，y1)，Q(5，y2)两点在此函数图像上，试比较y1，y2的大小

【题目】如图，已知，是一次函数的图象和反比例函数的图象的两个交点．

（1）求反比例函数和一次函数的解析式；

（2）求△的面积；

【题目】嘉淇正在参加全国“数学竞赛”，只要他再答对最后两道单选题就能顺利过关，其中第一道题有3个选项，第二道题有4个选项，而这两道题嘉淇都不会，不过嘉淇还有一次“求助”没有使用（使用“求助”可让主持人去掉其中一题的一个错误选项）．

（1）如果嘉淇第一题不使用“求助”，随机选择一个选项，那么嘉淇答对第一道题的概率是多少？

（2）若嘉淇将“求助”留在第二题使用，请用画树状图或列表法求嘉淇能顺利过关的概率；

（3）请你从概率的角度分析，建议嘉洪在第几题使用“求助”，才能使他过关的概率较大．

【题目】如图，在△ABC中，∠C=90°,AE平分∠BAC交BC于点E,O是AB上一点，经过A,E两点的⊙O交AB于点D，连接DE，作∠DEA的平分线EF交⊙O于点F，连接AF.

（1）求证：BC是⊙O的切线；

（2）若sin∠EFA=,AF=,求线段AC的长.

【题目】二次函数的图象如图所示，则下列结论：①；②；③；④；⑤的解为，其中正确的有（ ）

A. 5个 B. 4个 C. 3个 D. 2个

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网