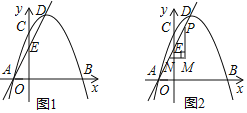��Ŀ����
����Ŀ����ͼ�٣���֪������y=ax2+bx+3��a��0����x�ύ�ڵ�A��1��0���͵�B��-3��0������y�ύ�ڵ�C��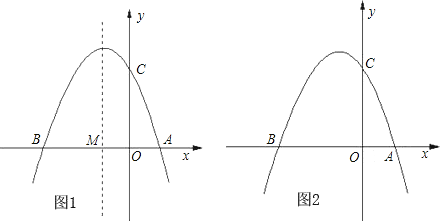
��1���������ߵĽ���ʽ��
��2���������ߵĶԳ�����x�ύ�ڵ�M�����ڶԳ������Ƿ���ڵ�P��ʹ��CMPΪ���������Σ������ڣ���ֱ��д�����з��������ĵ�P�����ꣻ�������ڣ���˵�����ɣ�
��3����ͼ�ڣ�����EΪ�ڶ�������������һ���㣬����BE��CE�����ı���BOCE��������ֵ�������ʱE������꣮
���𰸡���1��y=-x2-2x+3����2�����ڣ�P��-1��![]() ����P��-1��-
����P��-1��-![]() ����P��-1��6����P��-1��
����P��-1��6����P��-1��![]() ������3����a=-
������3����a=-![]() ʱ��S�ı���BOCE��������ֵΪ
ʱ��S�ı���BOCE��������ֵΪ![]() ����ʱ����E����Ϊ��-
����ʱ����E����Ϊ��-![]() ��
��![]() ����
����
��������
��1����֪�����߹�A��B���㣬�ɽ������������������ߵĽ���ʽ�У��ô���ϵ��������������κ����Ľ���ʽ��
��2���ɸ��ݣ�1���ĺ�������ʽ�ó������ߵĶԳ��ᣬҲ�͵ó���M������꣬����C����������y��Ľ��㣬���C������Ϊ��0��3��������M��C����������CM�ľ��룮Ȼ�����������������ۣ�
�ٵ�CP=PMʱ��Pλ��CM�Ĵ�ֱƽ�����ϣ���P������ؼ�����P�������꣬��P��PQ��y����Q�������PM=CP=x����ôֱ��������CPQ��CP=x��OM�ij����ɸ���M������ó���CQ=3-x����˿ɸ��ݹ��ɶ������x��ֵ��P��ĺ�������M�ĺ�������ͬ��������Ϊx���ɴ˿ɵó�P�����꣮
�ڵ�CM=MPʱ������CM�ij��������P�������꣬Ҳ�͵ó���P�����꣨Ҫע����������㣩��
�۵�CM=CPʱ����ΪC������Ϊ��0��3������ôֱ��y=3�ش�ֱƽ��PM�����P����������6���ɴ˿ɵó�P�����ꣻ
��3�������ı���BOCE���ǹ�����ı��Σ���˿ɽ��ı���BOCE�ָ�ɹ����ͼ�ν��м��㣬��E��EF��x����F��S�ı���BOCE=S��BFE+S����FOCE��ֱ������FOCE�У�FOΪE�ĺ�����ľ���ֵ��EFΪE�������꣬��֪C�������꣬��֪����OC�ij����ڡ�BFE�У�BF=BO-OF����˿���E�ĺ������ʾ��BF�ij�������������������E�����꣬Ȼ�����������߶��У����ɵó������ı���BOCE�������E�ĺ�����ĺ�����ϵʽ�����ݺ��������ʼ�������ı���BOCE�����ֵ����Ӧ��E�ĺ������ֵ�����������ʱE�����꣮
(1)��������y=ax2+bx+3(a��0)��x�ύ�ڵ�A(1,0)�͵�B(3,0)��
��![]()
��ã�![]() .
.
�����������߽���ʽΪ��y=x22x+3��
(2)�������߽���ʽΪ��y=x22x+3��
����Գ���Ϊ![]() ��
��
����P������Ϊ(1,a)����x=0ʱ��y=3��
��C(0,3),M(1,0)
�൱CP=PMʱ,(1)2+(3a)2=a2,���a=![]() ��
��
��P��������![]() ��
��
�൱CM=PMʱ,(1)2+32=a2,���![]() ��
��
��P��������![]() ��
��![]() ��
��
�൱CM=CPʱ,�ɹ��ɶ����ã�(1)2+32=(1)2+(3a)2�����a=6��
��P��������P4 (1,6).
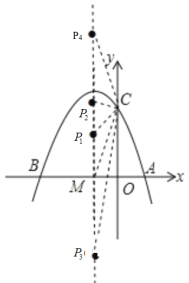
�����������ڷ��������ĵ�P,������Ϊ![]() ��
�� ![]() ��P(1,6)��
��P(1,6)��![]() ��
��
(3)����E��EF��x���ڵ�F,��E(a,a22a+3)(3<a<0)
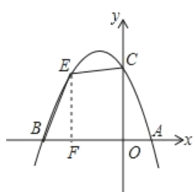
��EF=a22a+3��BF=a+3��OF=a
��![]()
![]()
![]()
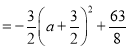
�൱a=![]() ʱ,S�ı���BOCE���,�����ֵΪ
ʱ,S�ı���BOCE���,�����ֵΪ![]() .
.
��ʱ,��E����Ϊ![]() .
.

 ��ǰ����ϵ�д�
��ǰ����ϵ�д�