题目内容
11.如图,一次函数y=-$\frac{1}{2}$x+2分别交y轴、x轴于A、B两点,抛物线y=-x2+bx+c过A、B两点.
(1)求这个抛物线的解析式;
(2)作垂直x轴的直线x=t,在第一象限交直线AB于M,交这个抛物线于N.求当t取何值时,四边形OANB的面积有最大值?最大值是多少?
(3)在(2)的情况下,设点P为直线x=t上的一个动点,求使△APB为直角三角形的点P的坐标.
分析 (1)由一次函数可求得A、B坐标,代入可求得抛物线解析式;
(2)用t可分别表示出M、N的坐标,则可表示出MN的长度,由于△OAB不变,故当△ABN面积最大时,四边形OANB的面积最大,用t可表示出△ABN的面积,利用二次函数的性质可求得答案;
(3)由(2)可求得t的值,可设出P点坐标,从而表示出PA、PB和AB的长,再分∠PAB=90°、∠PBA=90°和∠APB=90°三种情况利用勾股定理分别得到方程,可求得P点坐标.
解答 解:
(1)在y=-$\frac{1}{2}$x+2中,令x=0可得y=2,令y=0可求得x=4,
∴A(0,2),B(4,0),
∵抛物线y=-x2+bx+c过A、B两点,
∴$\left\{\begin{array}{l}{c=2}\\{-16+4b+c=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{b=\frac{7}{2}}\\{c=2}\end{array}\right.$,
∴抛物线解析式为y=-x2+$\frac{7}{2}$x+2;
(2)由题意可知N(t,-t2+$\frac{7}{2}$t+2),M(t,-$\frac{1}{2}$t+2),
∵M、N在第一象限,
∴MN=-t2+$\frac{7}{2}$t+2-(-$\frac{1}{2}$t+2)=-t2+4t=-(t-2)2+4,
∵-1<0,
∴当t=2时,MN有最大值,最大值为4,
∵A(0,2),B(4,0),
∴S四边形OANB=S△OAB+S△NAB=$\frac{1}{2}$OA•OB+$\frac{1}{2}$MN(4-0)=$\frac{1}{2}$×2×4+2[-(t-2)2+4]=-2(t-2)2+12,
∴当t=2时,四边形OANB的面积最大,最大值为12;
(3)由(2)可知t=2,
∴可设P(2,m),
∴PA2=(2-0)2+(m-2)2=m2-4m+8,PB2=(2-4)2+(m-0)2=m2+4,AB2=22+42=20,
∵△PAB为直角三角形,
∴有∠PAB=90°、∠PBA=90°和∠APB=90°三种情况,
①当∠PAB=90°时,则有PA2+AB2=PB2,
∴m2-4m+8+20=m2+4,解得m=6,
∴P(2,6);
②当∠PBA=90°时,则有PB2+AB2=PA2,
∴m2+4+20=m2-4m+8,解得m=-4,
∴P(2,-4);
③当∠APB=90°时,则有PA2+PB2=AB2,
∴m2-4m+8+m2+4=20,解得m=1+$\sqrt{5}$或m=1-$\sqrt{5}$,
∴P(2,1+$\sqrt{5}$) 或P(2,1-$\sqrt{5}$),
综上可知P点坐标为(2,6)或(2,-4)或(2,1+$\sqrt{5}$)或(2,1-$\sqrt{5}$).
点评 本题为二次函数的综合应用,涉及待定系数法、二次函数的最值、三角形的面积、勾股定理、方程思想及分类讨论.在(1)中求得A、B两点的坐标即可,在(2)中用t表示出MN的长度是解题的关键,在(3)用P点坐标分别表示出PA、PB的长是解题的关键,注意分情况讨论.本题考查知识点较多,综合性较强,难度适中.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案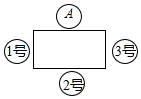 合作小组的4位同学坐在课桌旁讨论问题,学生A的座位如图所示,学生B,C,D随机坐到其他三个座位上,则学生B坐在2号座位的概率是( )
合作小组的4位同学坐在课桌旁讨论问题,学生A的座位如图所示,学生B,C,D随机坐到其他三个座位上,则学生B坐在2号座位的概率是( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{12}$ |
| x(元) | 10 | 15 | 20 | … |
| y(件) | 30 | 25 | 20 | … |
(1)求出日销售量y(万件)与销售价x(元)的函数关系式;
(2)若每日的销售利润为w(万元),要使每日的销售利润最大,每件产品的销售价应为多少元?此时每日销售利润是多少?
 如图,在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度,△ABC位于第二象限.
如图,在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度,△ABC位于第二象限.