题目内容
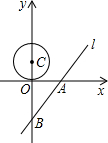如图所示，已知直线l的解析式是y=| 4 |
| 3 |
| A、6秒或10秒 |
| B、6秒或16秒 |
| C、3秒或16秒 |
| D、3秒或6秒 |
分析：先求得AB两点的坐标，再分两种情况：圆心C在点B上方和下方，可证出△BDE∽△BOA，△BFG∽△BAO，根据相似三角形的性质，求得BE，BF，再根据圆的移动速度，求出移动的时间．
解答：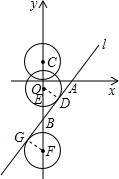
解：令x=0，得y=-4；
令y=0，解得x=3；
∴A（3，0），B（0，-4），
∴AB=5，
∵DE⊥l，GF⊥l，
∴△BDE∽△BOA，△BFG∽△BAO，
∴
=
，
=
，
即
=
，
=
，
解得BE=2.5，BF=2.5，
∴圆移动的距离为3或8，
∵圆心C从点（0，1.5）开始以每秒0.5个单位的速度沿着y轴向下运动，
∴移动的时间为6s或16s．
故选B．
解：令x=0，得y=-4；令y=0，解得x=3；
∴A（3，0），B（0，-4），
∴AB=5，
∵DE⊥l，GF⊥l，
∴△BDE∽△BOA，△BFG∽△BAO，
∴
| DE |
| OA |
| BE |
| AB |
| GF |
| OA |
| BF |
| AB |
即
| 1.5 |
| 3 |
| BE |
| 5 |
| 1.5 |
| 3 |
| BF |
| 5 |
解得BE=2.5，BF=2.5，
∴圆移动的距离为3或8，
∵圆心C从点（0，1.5）开始以每秒0.5个单位的速度沿着y轴向下运动，
∴移动的时间为6s或16s．
故选B．
点评：本题是一道关于一次函数的综合题，考查了切线的性质和一次函数的图象与几何变换，掌握分类讨论思想是解此题的关键．
练习册系列答案
名校课堂系列答案
相关题目
三角形？若存在，求出点C的坐标，并证明；若不存在，请说明理由．
4、如图所示，已知直线a∥b，被直线L所截，如果∠1=69°36′，那么∠2=
平移，设平移过程中△F′O′G′与四边形ODCE重叠部分面积为y，OO′的长为x（0≤x≤1），求y与x的函数关系式．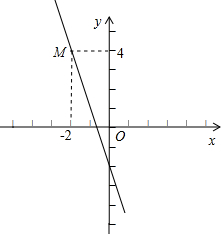
如图所示，已知直线y=kx-2经过M点，求此直线与x轴交点坐标和直线与两坐标轴围成三角形的面积．
如图所示：已知直线y=