题目内容
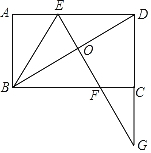
【题目】如图,已知矩形ABCD,对角线BD的垂直平分线分别交AD,BC和BD于点E,F,O.EF,DC的延长线交于点G,且OD=CG,连接BE.
(1)求证:△DOE≌△GCF;
(2)求证:BE平分∠ABD.
【答案】(1)详见解析;(2)详见解析.
【解析】
(1)由AAS即可得出△DOE≌△GCF;
(2)证△DOE≌△BOF(AAS),得出DE=BF,求出AE=CF=OE,即可得出结论.
证明:(1)∵EF是BD垂直平分线,
∴∠EOD=90°,
在矩形ABCD中,AD∥BC,∠A=∠BCD=90°,
∴∠DEO=∠GFC,∠DEO=∠BFO,∠FCG=90°,
∴∠EOD=∠FCG,
在△DOE和△GCF中,
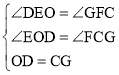 ,
,
∴△DOE≌△GCF(AAS);
(2)由(1)得:△DOE≌GCF,
∴OE=CF,
∵EF是BD垂直平分线,
∴OB=OD,
在△DOE和△BOF中,
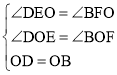 ,
,
∴△DOE≌△BOF(AAS),
∴DE=BF,
∵AD=BC,
∴AE=CF=OE,
又∵EA⊥BA,EO⊥BO,
∴BE平分∠ABD.

练习册系列答案
相关题目