题目内容
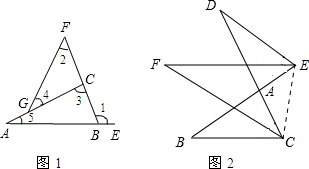 (1)如图1,请确定∠1与∠2的大小关系,并说明为什么?
(1)如图1,请确定∠1与∠2的大小关系,并说明为什么?(2)如图2,BE,CD相交于点A,∠DEA,∠BCA的平分线相交于F.探求∠F与∠B,∠D有何等量关系?(提示:连接CE)
分析:(1)先根据∠3是△CFG的外角确定出∠3与∠2的大小,再根据∠1是△ABC的外角确定出∠1与∠3的大小,进而可得出结论;
(2)由三角形内角和外角的关系可知∠D+∠1=∠3+∠F,∠2+∠F=∠B+∠4,由角平分线的性质可知∠1=∠2,∠3=∠4,故∠F=
(∠B+∠D).
(2)由三角形内角和外角的关系可知∠D+∠1=∠3+∠F,∠2+∠F=∠B+∠4,由角平分线的性质可知∠1=∠2,∠3=∠4,故∠F=
| 1 |
| 2 |
解答: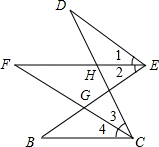 解:(1)∵∠3是△CFG的外角,
解:(1)∵∠3是△CFG的外角,
∴∠3>∠2,
∵∠1是△ABC的外角,
∴∠1>∠3,
∴∠1>∠2;
(2)∠F=
(∠B+∠D);
∵∠DHF是△DEH的外角,∠EHC是△FCH的外角,∠DHF=∠EHC,
∴∠D+∠1=∠3+∠F①
同理,∠2+∠F=∠B+∠4②
又∵∠1=∠2,∠3=∠4
∴①-②得:∠B+∠D=2∠F,即∠F=
(∠B+∠D).
 解:(1)∵∠3是△CFG的外角,
解:(1)∵∠3是△CFG的外角,∴∠3>∠2,
∵∠1是△ABC的外角,
∴∠1>∠3,
∴∠1>∠2;
(2)∠F=
| 1 |
| 2 |
∵∠DHF是△DEH的外角,∠EHC是△FCH的外角,∠DHF=∠EHC,
∴∠D+∠1=∠3+∠F①
同理,∠2+∠F=∠B+∠4②
又∵∠1=∠2,∠3=∠4
∴①-②得:∠B+∠D=2∠F,即∠F=
| 1 |
| 2 |
点评:本题考查的是三角形外角的性质及角平分线的性质,熟知三角形的外角等于与之不相邻的两个内角的和是解答此题的关键.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目






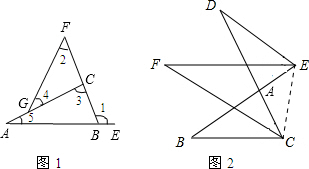 (1)如图1,请确定∠1与∠2的大小关系,并说明为什么?
(1)如图1,请确定∠1与∠2的大小关系,并说明为什么?