题目内容
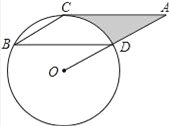
【题目】如图,点B、C、D都在⊙O上,过C点作CA∥BD交OD的延长线于点A,连接BC,∠B=∠A=30°,![]() .
.
(1)试说明:AC是⊙O的切线;
(2)求由线段AC、AD与弧CD所围成的阴影部分的面积.(结果保留π)
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)连接OC,根据圆周角定理求出∠COA,根据三角形内角和定理求出∠OCA,根据切线的判定推出即可.
(2)求出DE,解直角三角形求出OC,分别求出△ACO的面积和扇形COD的面积根据转换思想,由即![]() 可得出答案.
可得出答案.
试题解析:解:(1)证明:如答图,连接OC,交BD于E,
∵∠B和∠COD是同弧所对的圆周角和圆心角,∴∠COD=2∠B.
∵∠B=30°,∴∠COD=60°.
∵∠A=30°,∴∠OCA=90°,即OC⊥AC.∴AC是⊙O的切线.
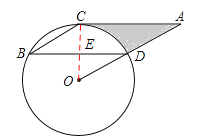
(2)∵AC∥BD,∠OCA=90°,∴∠OED=∠OCA=90°.
∵BD=![]() ,∴
,∴![]() .
.
∵在Rt△ODE中, ![]() ,∴OD=2.
,∴OD=2.
∵在Rt△ACO中, ![]() , ∴AC=
, ∴AC=![]() .
.
∴![]() .
.

练习册系列答案
相关题目