题目内容
【题目】如图已知正比例函数图像经过点A(2,3)、B(m,6).
(1)求正比例函数的解析式.
(2)求m的值及A、B两点之间的距离。
(3)分别过点A与点B作y轴的平行线,与反比例函数在第一象限内的分支分别交于点C、D(点C、D均在点A、B下方),若BD=5AC.求反比例函数的解析式,并求出四边形ACDB的面积。
【答案】(1)y=![]() x;(2)m=4;
x;(2)m=4;![]() ;(3)
;(3)![]() ;四边形ACDB的面积为6.
;四边形ACDB的面积为6.
【解析】
(1)设正比例函数的解析式为:y=kx(k≠0),然后将点A的坐标代入即可求出正比例函数的解析式;
(2)将B点坐标代入正比例函数解析式中即可求出m,然后根据平面直角坐标系中任意两点之间的距离公式,即可求出AB;
(3)设反比例函数的解析式为:![]() (a≠0),根据AC∥BD∥y轴,即可求出C、D的横坐标,根据反比例函数的解析式即可用a表示出C、D的纵坐标,从而求出BD和AC,然后列出方程即可求出a的值,从而求出反比例函数的解析式,然后根据梯形面积公式计算面积即可.
(a≠0),根据AC∥BD∥y轴,即可求出C、D的横坐标,根据反比例函数的解析式即可用a表示出C、D的纵坐标,从而求出BD和AC,然后列出方程即可求出a的值,从而求出反比例函数的解析式,然后根据梯形面积公式计算面积即可.
解:(1)设正比例函数的解析式为:y=kx(k≠0)
将点A(2,3)代入,得:3=2k
解得:![]()
故正比例函数的解析式为:y=![]() x;
x;
(2)将B点(m,6)代入y=![]() x中,得:6=
x中,得:6=![]() m
m
解得:m=4
根据平面直角坐标系中任意两点之间的距离公式:AB=![]() ;
;
(3)设反比例函数的解析式为:![]() (a≠0)
(a≠0)
∵AC∥BD∥y轴
∴A、C的横坐标相同,即点C的横坐标为:2, B、D的横坐标相同,即点D的横坐标为:4,
∴点C的纵坐标为![]() ,点D的纵坐标为
,点D的纵坐标为![]()
∴AC=3-![]() ,BD=6-
,BD=6-![]()
∵BD=5AC
∴6-![]() =5(3-
=5(3-![]() )
)
解得:a=4
∴反比例函数的解析式为:![]() .
.
过点C作CE⊥BD于E
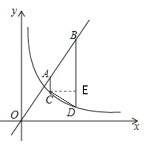
∴AC=1,BD=5,CE=4-2=2
∴S梯形ACDB=![]() =6.
=6.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目