题目内容
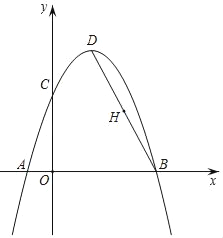
【题目】如图，直线y=kx﹣3（k≠0）与坐标轴分别交于点C，B，与双曲线y=﹣
（x＜0）交于点A（m，1），则AB的长是（ ）
A. 2
B. 
C. 2
D. 
【答案】A
【解析】
由A为直线y=kx﹣3（k≠0）与双曲线y=﹣
（x＜0）的交点可求得A点坐标与一次函数的解析式，可求得B点坐标，用两点间距离公式可求得AB的长.
解：A为直线y=kx﹣3（k≠0）与双曲线y=﹣（x＜0）的交点，可得A满足双曲线的解析式，可得：
，解得：
，即A点坐标为（-2，1）,
A点再直线上，可得A点满足y=kx﹣3（k≠0），
可得：
，解得：k=-2，
一次函数的解析式为：y=-2x﹣3，
B为直线与y轴的交点，可得B点坐标（0，-3），
由A点左边（-2，1），
可得AB的长为
=
，
故选A.
练习册系列答案
阅读快车系列答案
相关题目
【题目】某日王老师佩戴运动手环进行快走锻炼，两次锻炼后数据如表．与第一次锻炼相比，王老师第二次锻炼步数增长的百分率是其平均步长减少的百分率的3倍．设王老师第二次锻炼时平均步长减少的百分率为
．
项目 | 第一次锻炼 | 第二次锻炼 |
步数(步) | 10000 | ____________ |
平均步长(米/步) | 0.6 | ____________ |
距离(米) | 6000 | 7020 |
注：步数×平均步长＝距离．
(1)根据题意完成表格填空；
(2)求x；
(3)王老师发现好友中步数排名第一为24000步，因此在两次锻炼结束后又走了500米，使得总步数恰好为24000步，求王老师这500米的平均步长．
